Capitolo 2 – Lo spazio e il tempo

Apriamo questo capitolo con il seguente esempio. Supponete di trovarvi in un periodo storico in cui, per vari motivi, c’era l’assoluta convinzione che la terra fosse piatta e provate a spiegare ad un abitante di quel periodo che la terra è molto simile ad una sfera schiacciata ai poli. Credo che nonostante le vostre conoscenze e nonostante il vostro impegno, alla fine non riuscirete a convincerlo. Vi chiedete perché? Semplicemente per l’oggettiva difficoltà di sradicare un pregiudizio profondo. Nonostante le prove che voi cercherete di portare a vostro favore, il vostro interlocutore alla fine se ne andrebbe ridendo delle vostre convinzioni. Comunque, cerchiamo di capire perché in diversi periodi storici si pensava che la terra fosse piatta. Innanzitutto c’erano le esperienze di vita vissuta (che davano la sensazione di un mondo piatto) e poi le cartine geografiche. E voi direte: e che c’entrano le cartine geografiche in questo discorso? C’entrano, c’entrano e come se c’entrano! Il fatto di rappresentare la terra su una superficie piatta (il foglio), ha un effetto collaterale indesiderato, cioè di affermare implicitamente che ciò che si sta rappresentando sia effettivamente piatto proprio come il foglio. In realtà, non avendo alcuna informazione su ciò che si sta rappresentando, nessuno ci autorizza a prendere una superficie piatta come base dei nostri schemi. Infatti, se facciamo una cartina geografica di tutto il planisfero (senza portare in conto che la superficie della terra non è piatta) faremo un grosso errore e la cartina risulterà sbagliata. Per poter rappresentare una superficie curva su una superficie piana, dobbiamo prima effettuare dei “tagli” sulla superficie curva, per poi schiacciare la superficie curva sul piano. Questo perché le aree che schiacciamo sul piano possono essere approssimate come superfici piane solo fino ad una certa estensione. Oltre questa estensione, è inevitabile che la superficie non è più assimilabile ad una superficie piana. Prendete ad esempio un grande parcheggio. La sua area è visibilmente piana, eppure si trova sulla superficie del nostro pianeta che piatto non è. Questo perché fino a certe estensioni dire che una superficie è piana o leggermente incurvata fa poca differenza.

Ad esempio nella seguente figura,

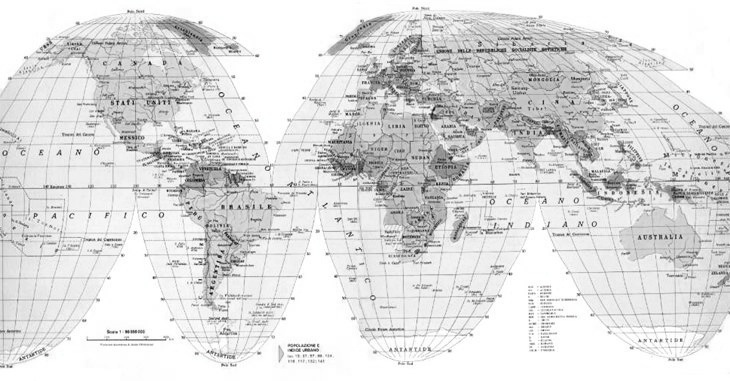
si vede chiaramente che si sono fatti dei “tagli” sul mappamondo, per poterlo schiacciare sul piano, al fine di mantenere coerente la rappresentazione con ciò che c’è nella realtà. Però ciò non significa affatto che lo spazio bianco che si è venuto a creare sul piano esista davvero nella realtà. Tale spazio viene a formarsi soltanto quando si rappresenta la superficie terrestre su un piano, ma non ha nessun riscontro effettivo nel mondo reale. Un altro esempio si può fare usando la buccia di un’arancia. Prendete un’arancia e tagliatela in sette spicchi uguali. Togliete la polpa dell’arancia in modo da lasciare di ogni spicchio solo la buccia. Avrete quindi la buccia tagliata in sette spicchi uguali. Fate ora aderire la buccia sul piano. Affiancate le varie fettine delle bucce e otterrete qualcosa che più o meno simile alla seguente figura.

Nel momento in cui noi vogliamo ritornare alla vera struttura di partenza, dobbiamo eliminare lo spazio che si forma per effetto dello schiacciamento nel piano (l’area bianca) e “ricucire” i vari lembi in modo da riottenere la forma sferica da cui partivamo. Se ci ostinassimo a voler considerare anche lo spazio bianco, avremo delle incongruenze fisiche. Nella fattispecie, avremmo che l’area totale sarebbe molto maggiore di quella reale e che punti contigui sulla superficie sferica (ad esempio A e A’) diventerebbero magicamente molto distanti tra loro.

E’ importante che il lettore abbia ben chiaro questo concetto, perché tra poco lo sposteremo su un qualcosa di un po’ più complicato… lo spaziotempo. E’ vero che tutte queste cose possano sembrare delle osservazioni banali, ma come avete avuto modo di notare dal capitolo precedente, da tante piccole banalità si sono dedotte delle cose non banali.

Ora prendiamo un oggetto qualsiasi che si muove in linea retta e a velocità costante. Vogliamo farne una rappresentazione che sia il più possibile coerente con la realtà. Alle scuole, e alle università ci insegnano che per rappresentare un moto del genere, dobbiamo prendere un sistema di riferimento cartesiano nel piano, assegnare all’asse delle ascisse il tempo e a quello delle ordinate lo spazio. Ma prima di procedere oltre, è necessario porsi alcune domande: chi ci autorizza ad utilizzare il piano per una rappresentazione dello spaziotempo? Ed inoltre: chi ci garantisce che lo spazio e il tempo siano veramente lineari? E per finire: chi ci garantisce che lo spazio e il tempo siano perpendicolari fra loro? Come avrete ben capito, nessuno ci può confermare o smentire a priori che le nostre scelte siano giuste o sbagliate; solo successivamente, quando ci saremmo accorti di eventuali concordanze, o incongruenze potremmo dire con una certa sicurezza se il modello che avevamo scelto era corretto o no.

Per evitare che qualche lettore si perda per strada, facciamo una piccola digressione sui riferimenti cartesiani; gli altri lettori, se non vogliono annoiarsi, possono saltare più avanti…..

Il sistema di riferimento cartesiano, fu introdotto dal matematico Renato Cartesio, (da cui il nome cartesiano). Egli si accorse che, all’interno di una stanza, poteva individuare tutti i punti della stanza, semplicemente con tre numeri, che sono rispettivamente la distanza dal pavimento, la distanza da una parete e la distanza dall’altra parete (adiacente a quella precedente). La stanza in questione, la possiamo immaginare come una scatola (ad esempio un cubo). Due facce adiacenti, si incontrano a formare uno spigolo (che è un segmento lineare). Tre spigoli si incontrano formando un vertice, che di fatto è un punto. Ad esempio qui di seguito abbiamo messo un sistema di riferimento a tre dimensioni nello spazio.

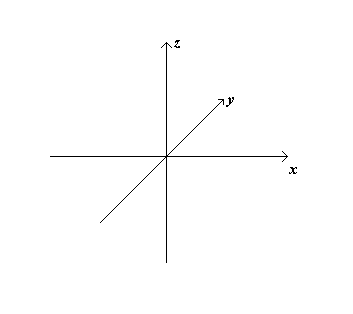
Prendiamo ora un sistema di riferimento cartesiano nel piano. Per convenzione si indica con la lettera x la retta denominata asse delle ascisse, mentre si indica con la lettera y la retta denominata con il nome di asse delle ordinate. Sempre per convenzione, si sceglie un verso positivo sia per l’asse delle ascisse sia per quello delle ordinate. Il verso positivo per le ascisse è quello che va da sinistra verso destra, mentre per l’asse delle ordinate è quello che va dal basso verso l’alto. Questa cosa si evidenzia mettendo una freccia a destra sull’asse delle ascisse e una freccia verso l’alto per l’asse delle ordinate. Il punto dove le due rette si incrociano si chiama origine o anche origine degli assi. Questo punto è lo zero per l’ascissa x e lo zero per l’ordinata y, cioè vuol dire che se da questo punto ci spostiamo verso destra i numeri riportati sull’asse delle x aumenteranno positivamente, se invece ci spostiamo verso sinistra aumenteranno negativamente. Insomma, è come lo zero di un termometro. Al di sotto dello zero abbiamo le temperature negative. Analogamente per l’asse delle ordinate. Andando verso l’alto aumenteranno positivamente, scendendo verso il basso aumenteranno negativamente. Pertanto il nostro riferimento cartesiano nel piano sarà fatto in questo modo:

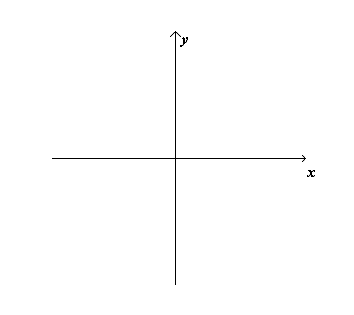
Nelle scuole c’insegnano che per fare una rappresentazione del moto di un oggetto dobbiamo procedere come segue: 1) prendere un sistema di riferimento cartesiano come quello precedente; 2) sostituire l’asse delle ascisse x, con il tempo t e l’asse delle ordinate y, con spazio. In altre parole abbiamo quello che è rappresentato nella figura seguente:

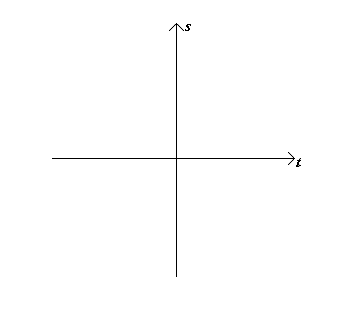
Su questo sistema di riferimento i punti del piano sono le coordinate spazio-temporali. Invece, una qualsiasi linea, retta o curva, rappresenta quello che normalmente in fisica si chiama “linea d’universo di un osservatore”, cioè il percorso nello spazio e nel tempo che compie un osservatore. In particolare, in questa sede, siamo interessati alle linee d’universo di tipo rettilinee. Infatti una qualsiasi retta disegnata nel piano s-t rappresenta un osservatore che si muove a velocità costante. Le rette passanti per l’origine degli assi (il punto in cui si incontrano le rette “s” e “t“) sono del tutto equivalenti a quelle che non passano per l’origine, ma hanno il vantaggio di passare per il punto di coordinate s = 0 e t = 0; il che è solo una questione di scelta dei riferimenti, ma semplifica i ragionamenti. Di seguito, abbiamo rappresentato un grafico s-t con alcune rette passanti per l’origine.

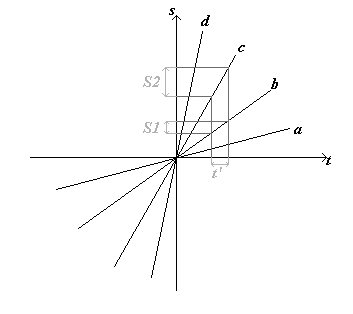
Ora facciamo alcune considerazioni sul grafico. Abbiamo già detto che le linee d’universo rettilinee rappresentano un osservatore che si muove a velocità costante. Cerchiamo di capire il perché di tutto questo, confrontando le rette contrassegnate con le lettere “a“, “b“, “c” e “d“. Come esempio prendiamo le rette “b” e “c“. Prendiamo un intervallo di tempo t’. Spostiamo quest’intervallo verso l’alto (parallelamente all’asse dello spazio “s“). Gli estremi dell’intervallo incontrano prima la retta “b” e poi la retta “c“. Quando incontriamo la retta “b“, effettuiamo una seconda traslazione verso sinistra e quando incontriamo la retta “c” effettuiamo un’altra traslazione verso sinistra. In questo modo stiamo controllando quanto spazio hanno percorso i due osservatori nello stesso intervallo di tempo. Ora da un rapido controllo si vede che l’osservatore della retta “b” ha percorso uno spazio “S1“, mentre l’osservatore della retta “c” ha percorso lo spazio “S2“. E’ facile vedere che “S2” è più grande di “S1“; pertanto l’osservatore “c” (nello stesso intervallo di tempo) ha percorso più spazio dell’osservatore “b“. Possiamo quindi dire che l’osservatore “c” è più veloce dell’osservatore “b”. Allo stesso modo ci possiamo rendere conto che l’osservatore “b” è più veloce dell’osservatore “a“, e che l’osservatore “d” è più veloce dell’osservatore “c“. In altre parole essere più veloce di un altro osservatore equivale a dire che la propria linea d’universo (sul grafico s-t) è una retta che risulta essere più vicina all’asse dello spazio “s“. Spieghiamoci meglio: prendete una retta sul grafico s-t (passante per l’origine); fatela ruotare in senso antiorario. Più questa si avvicina all’asse spaziale e più significa che state andando molto veloci. Se spingete il ragionamento al limite (cioè la retta che avete preso si sovrappone all’asse “s“) allora avrete un osservatore che possiede velocità infinita; mentre se la fate ruotare in senso orario avrete un osservatore che è sempre più lento. Ancora una volta se spingete il ragionamento al limite (cioè la retta si sovrappone all’asse “t“) avrete che l’osservatore risulta fermo nel vostro sistema. di riferimento.

Capito questo fatto, facciamo un passo avanti. Proviamo a rappresentare nel piano s–t un oggetto che si muove a velocità uguale a quella della luce. Come tutti sanno, la luce si propaga all’incirca a 300.000 Km al secondo. Disegnare, la linea d’universo di un oggetto che si muove ad una velocità così elevata non è molto facile, se non altro per l’oggettiva difficoltà di fare in modo che questa linea sia distinguibile dalla retta “s“; infatti le due rette risulterebbero talmente vicine, che nessun grafico in scala permetterebbe di poter distinguere l’una dall’altra. Per una chiarezza d’esposizione, facciamo una piccola forzatura; disegneremo la linea d’universo dell’osservatore che si muove alla velocità della luce un po’ discostata dalla retta “s” per fare in modo che le due rette siano distinguibili. Questo tipo di “forzatura” serve soltanto per rendere i disegni più comprensibili e non c’è nessun’altra controindicazione. Oltre a questa linea d’universo, vogliamo anche disegnare quella di un altro osservatore che si muove sempre a velocità della luce, ma nella direzione opposta a quella dell’altro osservatore. Nel grafico seguente abbiamo contrassegnato con la lettera “c” l’osservatore che si muove alla velocità della luce nel verso positivo dell’asse delle ordinate, mentre è stata contrassegnata con la lettera “-c” l’osservatore che si muove con velocità della luce, ma nella direzione opposta. Le frecce poste a fianco a ciascuna retta aiutano meglio a visualizzare questo fatto.

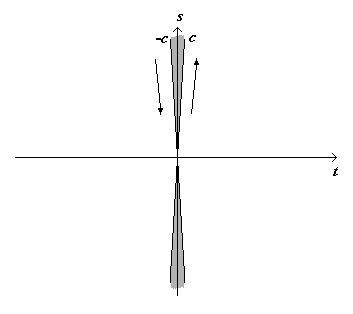
L’area colorata in grigio rappresenta una zona in cui le linee di universo degli osservatori sono evidentemente superiori a quelle della luce (sia in un verso che nell’altro). Dalla teoria della relatività ristretta e degli esperimenti sappiamo che la velocità della luce è un limite invalicabile e pertanto niente può superare tale velocità. Ora poiché nessun corpo fisico può superarla, viene da chiedersi se questa zona esista realmente o sia il frutto di uno schiacciamento nel piano di uno spazio tempo curvo. In questo caso facciamo un esplicito riferimento agli esempi del mappamondo e della buccia d’arancia che veniva schiacciata nel piano. Infatti, poiché il diagramma spazio-tempo fatto sul piano ci ha portato ad un’incongruenza fisica, ci sembra quasi naturale pensare che lo spazio-tempo sia in realtà una superficie curva. In questo caso stiamo deducendo la sua curvatura dello spaziotempo senza fare un uso esplicito della teoria della relatività generale. L’unico ingrediente che abbiamo inserito dentro è quello che ci dice che la velocità della luce non può essere superata, che fa parte solo della relatività ristretta. Pertanto la zona colorata in grigio, nella realtà, non esiste; allora è necessario toglierla. Se tagliamo via quest’area e ricuciamo i lembi, otteniamo una superficie curva che finisce come la punta di un cono verso il centro. Il lettore può convincersi di questo fatto notando che le due aree grigie convergono in modo brusco verso l’origine degli assi. Questo è dovuto al fatto che stiamo esaminando un’area data dall’incrocio di due rette e pertanto, nel punto di incontro, creano disomogeneità e curvatura differente. Invece, poiché tutti i punti dell’universo dovrebbero avere uguale curvatura, per il fatto che non esistono punti privileggiati, se ne deduce che è stato commesso qualche errore. L’errore che è stato fatto è quello di aver considerato tutte le linee d’universo come se fossero lineari, in particolare le linee d’universo degli osservatori che viaggiano alla velocità della luce. Ciò ci porta a pensare che queste dovrebbero essere delle curve che, in particolari condizioni, possono essere considerate delle rette. In geometria analitica si osserva che la cosiddetta “equazione canonica” della circonferenza, degenera in una retta se la circonferenza tende all’infinito. Questi “parole” così complicate, stanno ad indicare che se una circonferenza diventa grandissima, un pezzo di essa ci “appare” come se fosse un pezzo di una retta; ancora una volta, spingendo il ragionamento al limite, se la circonferenza diventa infinita, la circonferenza stessa diventa una retta.

Capito questo, ci rendiamo conto che è necessario sostituire le linee d’universo (associate alla luce) con delle linee curve, ad esempio potremmo pensare a degli archi di circonferenza . Quindi la situazione può diventare pertanto la seguente:

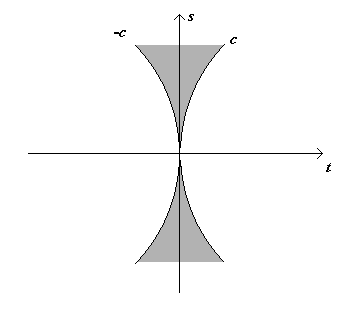
Abbiamo volutamente accentuato la curvatura delle linee d’universo, per mettere in evidenza che “c” e “-c” non sono rette, ma archi di circonferenza, ma avremmo potuto scegliere anche degli archi parabolici. Per il momento, non avendo altre informazioni, procediamo con l’ipotesi degli archi di circonferenza e vediamo dove arriviamo. Ovviamente, nella realtà, la curvatura è tale da far sì che queste linee d’universo siano confondibili con delle rette. Infatti, più una circonferenza è grande, e più è facile che un tratto di questa circonferenza assomigli molto ad una retta. Una cosa simile accade per la terra. Essendo il raggio della terra di 6380 Km circa, ecco che un tratto di superficie terrestre, pur essendo curva, venga confusa per piana. Ora, se ripetiamo nuovamente il ragionamento precedente, ci accorgiamo che non esistono più dei punti particolari, ma la superficie curva che ne deriva è abbastanza omogenea. A questo punto potremmo credere di aver finito e che richiudendo il tutto otteniamo la forma dello spazio-tempo…. ma invece manca ancora qualcosa! Al nostro modellino dello spazio-tempo gli abbiamo detto che la velocità della luce non è superabile (e lui ci ha risposto dicendoci che la superficie dello spazio-tempo deve essere curva); gli abbiamo detto che lo spazio-tempo deve essere omogeneo e non ci devono essere punti in cui si vede qualcosa di diverso rispetto agli altri (e lui ci ha detto che le linee d’universo della luce devono essere delle curve come ad esempio degli archi di circonferenza). L’unica cosa che non gli abbiamo detto è che il tempo scorre in un solo verso. Facciamo a tal proposito una piccola digressione. Riprendiamo il grafico s–t; disegniamo in esso due linee d’universo di due osservatori; uno si muove in un verso, l’altro si muove nel verso opposto.

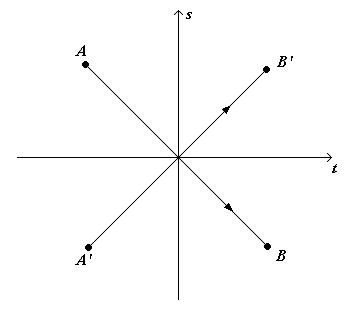
Abbiamo l’osservatore che va da A verso B, e quello che va da A’ verso B’. Ovviamente non è possibile che il primo osservatore percorra la linea d’universo da B verso A, né che il secondo percorra la sua linea d’universo da B’ verso A’; in tal caso significherebbe che i due osservatori si sono mossi indietro nel tempo. Ci accorgiamo invece che i due percorsi sono l’uno l’inverso dell’altro (rispetto allo spazio). Infatti se ribaltiamo il foglio sottosopra, ci accorgiamo che il disegno che otteniamo è pressoché identico a quello di partenza., dove questa volta la direzione spaziale punta verso il basso del foglio. Così facendo abbiamo semplicemente invertito tutto il discorso rispetto allo spazio, mentre la freccia del tempo continua ad essere orientata verso destra. Se invece, partendo dal disegno della pagina precedente, giriamo il foglio così come si gira la pagina di un libro, avremo ottenuto un ribaltamento rispetto al tempo. Se ora confrontiamo il disegno che si ottiene ribaltando il tempo, con quello di partenza, ci accorgiamo che, a parte le frecce che indicano il verso di percorrenza, il resto del grafico è perfettamente uguale. Cosa ne deduciamo? Che il grafico s-t è “muto” rispetto al tempo, cioè che tale grafico non ci dice da che parte scorre il tempo, perché ribaltare il grafico rispetto allo spazio o rispetto al tempo (in questo grafico) non fa nessuna differenza. Invece noi sappiamo che andare in una direzione o in quella opposta non equivale a muoversi indietro nel tempo. Vi facciamo un altro esempio. Supponete di guardare un filmato. Nel filmato si vede un pallone da calcio che si muove da sinistra verso destra. Siete in grado con questa semplice informazione di stabilire se il filmato viene proiettato nel verso giusto o se nel verso contrario? In altre parole un oggetto che si muove da sinistra verso destra è equivalente ad un oggetto che si muove da destra verso sinistra, ma nel tempo che scorre all’indietro? E’ un po’ contorta come domanda… ma non è così banale come si potrebbe pensare. Comunque la risposta a questa domanda è ovviamente: no, perché altrimenti invertire la direzione dei propri movimenti equivarrebbe ad andare indietro nel tempo… e purtroppo non è così semplice andare indietro nel tempo!

Quindi ne dobbiamo dedurre che nel grafico c’è qualcosa di sbagliato! Ma cosa? Abbiamo già detto che le linee d’universo sono archi circonferenza; abbiamo già detto che la superficie dello spazio-tempo è una superficie curva. Cosa ci manca? Chiederci se l’asse spaziale è veramente una retta, se quella del tempo è veramente una retta e se spazio e tempo sono davvero ortogonali fra loro.

Andiamo per gradi. Vediamo se l’asse spaziale è veramente una retta o una curva. Per far questo ci aiutiamo con il seguente ragionamento. Innanzitutto ricordiamo che il sistema di riferimento cartesiano risulta (per costruzione) suddiviso in quattro aree (o settori) uguali fra loro. Il disegno seguente spiega meglio questo fatto:

L’area più chiara (e contrassegnata con il numero 1), viene comunemente chiamata “primo quadrante”; l’area un po’ più scura (e contrassegnata con il numero 2), viene chiamata “secondo quadrante”; l’area ancora più scura (e contrassegnata con il numero 3) viene chiamata “terzo quadrante”; l’area più scura di tutte (e contrassegnata con il numero 4) viene chiamata “quarto quadrante”.

Detto questo, notiamo subito che la perfetta simmetria fra i vari quadranti sottintende automaticamente l’omogeneità dello spazio e del tempo, in particolare significa che passare dal secondo al quarto quadrante o dal quarto al secondo, è la stessa cosa. Se questa cosa è vera per lo spazio, non possiamo di certo dire la stessa cosa per quanto riguarda il tempo; in altre parole muoversi dal secondo al primo quadrante, non è del tutto equivalente a muoversi dal primo al secondo. Infatti, se nel primo caso ci muoviamo nel verso consueto del tempo, nel secondo caso ci dovremmo muovere indietro nel tempo, e evidentemente, quest’ultima cosa non è vera.

Pertanto, questo implica che tra il secondo e il primo quadrante ci deve essere un’asimmetria che ci renda conto del fatto che il tempo scorre in un solo verso. Lo stesso tipo di asimmetria ci deve essere tra il terzo e il quarto quadrante, perché, ovviamente, il tempo scorre nello stesso verso sia nel primo e nel secondo, che nel terzo e nel quarto. Invece, il passaggio dal primo al quarto quadrante deve essere equivalente al passaggio che c’è tra quarto e primo quadrante, perché in questo caso stiamo osservando la cosa dal punto di vista dello spazio e non dal punto di vista del tempo. Infatti, muoversi in una direzione è equivalente a muoversi nella direzione opposta (ovviamente in assenza di campi di forze).

Siamo quindi giunti alla conclusione che dobbiamo modificare il sistema di riferimento cartesiano al fine di ottenere uno spazio-tempo che sia congruente con la realtà. Tale modifica deve essere tale da fare in modo che sussistano le condizioni di simmetria spaziale e di asimmetria temporale. Come prima cosa ci viene subito in mente che per ottenere qualcosa di simile dobbiamo distorcere l’asse dello spazio. Ma come? E in che modo? Sicuramente dobbiamo fare in modo che, il nuovo asse spaziale sia tale da fare in modo che in tutti i punti dello spazio si veda la stessa cosa. Una possibile sostituzione che ci viene subito è quello di sostituirlo con un arco di circonferenza; infatti questa ha lo stesso tipo di curvatura ovunque, e ciò soddisferebbe le condizioni richieste. Ma l’arco di circonferenza come deve essere orientato? Esistono di fatto due possibilità: la prima con concavità rivolta verso il futuro, l’altra con concavità rivolta verso il passato. Di seguito le esaminiamo entrambe per cercare di capire quale delle due soddisfa meglio le condizioni reali. Cominciamo a disegnare qui di seguito quella con concavità rivolta verso il futuro.

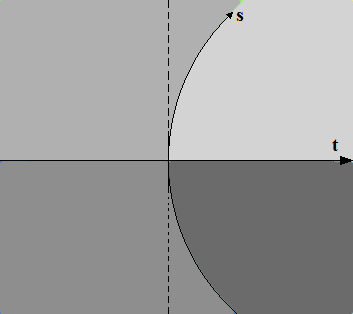
E’ possibile osservare che, ribaltare il disegno sottosopra e guardandolo dalla parte opposta si ottiene un disegno molto simile a quello di partenza; invece se giriamo il foglio dal lato lungo (così come si gira una pagina di un libro) e osserviamo il disegno otteniamo qualcosa che non è proprio identico al disegno di partenza. Questo significa che questo tipo di spazio-tempo è simmetrico per quanto riguarda lo spazio, ma non per quanto riguarda il tempo. Nel disegno, come al solito, abbiamo volutamente accentuato la curvatura dello spazio, che ovviamente non è così; anzi questa è talmente lieve da farci credere che lo spazio sia lineare e non curvo. Abbiamo disegnato invece con una linea tratteggiata quella che apparentemente sembra essere la linea spaziale. E’ possibile osservare che anche il disegno qui di seguito soddisfa le condizioni di simmetria spaziale e di asimmetria temporale:

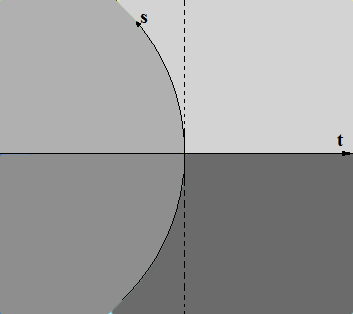
Come possiamo osservare i due disegni hanno una notevole differenza rispetto al tempo. Ma allora, quale dei due è corretto? Qual è quello che soddisfa tutte le condizioni del nostro spazio-tempo? Per rispondere a queste domande dobbiamo analizzare il moto di un corpo prima nel primo spazio e poi nel secondo e vedere quale dei due è più coerente. Nel grafico che segue abbiamo disegnato le curve “a” e “b” che sono due percorsi opposti di due osservatori distinti. Le curve “a” e “b” sono le linee d’universo di questi due osservatori che si muovono a velocità costante. La curvatura che esse possiedono deriva dal fatto che l’asse spaziale è curvato in avanti. Per ottenerle basta infatti ruotare la curva dello spazio “s“.

Notiamo anche che con la rotazione dell’asse curvo dello spazio, se ne modifica anche l’incurvamento. Infatti, eseguendo una rotazione di 90° in senso orario fino a raggiungere l’asse del tempo, dovremmo trovarci ad avere una retta come l’asse del tempo. Questo significa che mano a mano che la curva dello spazio ruota in senso orario, il suo incurvamento tende a schiacciarsi sempre di più fino a tornare ad essere una retta. Ma per il momento questa osservazione non la teniamo in conto. Invece le rette a’ e b’ sono i percorsi che si osservano se si suppone che lo spazio sia lineare. Pertanto, se osserviamo questo fenomeno da un sistema di riferimento classico (nella figura è quello contrassegnato da s’ e da t), i due osservatori non sembrano muoversi a velocità costante, ma sembrano muoversi di moto decelerato; l’effetto di questo spazio-tempo è quindi quello di rallentare il moto dei corpi. Chiameremo pertanto questo tipo di spazio-tempo “spazio decelerato”.

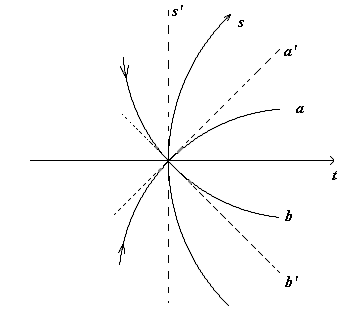
Vediamo ora l’altra possibilità, cioè quella della concavità rivolta verso il passato.

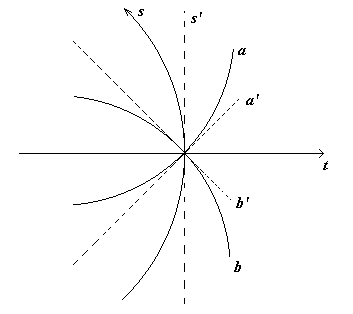
Anche in questo caso abbiamo preso gli osservatori “a” e “b” che si muovono a velocità costante. Ovviamente, come nel caso precedente, muoversi a velocità costante in uno spazio-tempo in cui l’asse spaziale è curvo, significa avere una linea d’universo curva. Se tale linea viene osservata da un sistema di riferimento classico appare (in questo caso) come un corpo in accelerazione. Chiameremo questo tipo di spazio-tempo “spazio accelerato”.

Ora dobbiamo cercare di capire quale dei due sistemi è più aderente al nostro universo. Nel primo caso abbiamo quindi (oltre alla gravità) anche un’altra forza attrattiva che tenderebbe a rallentare il movimento dei corpi. L’effetto complessivo di queste due forze dovrebbe essere quello di rallentare l’espansione dell’universo e di invertire il moto delle galassie.

Nel secondo caso, la forza generata dal piegamento dello spazio verso il passato fa sì che ci appaia come una forza repulsiva che accelera i corpi, mettendosi in contrapposizione alla gravità.

In particolare i due effetti (nello spazio accelerato) tendono ad annullarsi reciprocamente dando così l’idea di uno spazio-tempo pressoché piatto. Quest’ultima considerazione è in accordo con le rilevazioni sperimentali (esperimento BOOMERANG[1]) che danno un aspetto dell’universo abbastanza piatto e con altre osservazioni che vedono in accelerazione i corpi dell’universo più lontani.

Quindi d’ora in poi considereremo lo spazio accelerato come il modello aderente al tempo che scorre nel verso positivo (cioè quello conosciuto), mentre con lo spazio decelerato alluderemo al modello con il tempo negativo.

Vi vogliamo far notare che le curvature in questione sono state molto accentuate e che per intervalli di tempo piccoli (non superiori agli anni) e per lunghezze relativamente piccole (inferiori agli anni luce), il sistema di riferimento può essere approssimato con quello classico; l’unica differenza che esiste, è che sul sistema di riferimento classico l’inversione temporale non cambia nulla, mentre nel sistema “spazio accelerato” cambia totalmente la situazione. Anzi più gli spazi diventano piccoli e più queste asimmetrie si noteranno sempre di meno fino quasi a scomparire, questo perché se si prende una porzione di una curva e la si sceglie molto piccola, sembrerà tanto più lineare quanto più piccola è questa porzione di curva. Ciò vuol dire che nel mondo del microcosmo, ovvero quello della meccanica quantistica, i fenomeni devono apparire come se ci fosse una perfetta simmetria tra passato e futuro e quindi come se non ci non fossero differenze tra oggetti che si muovono avanti nel tempo ed oggetti che si muovono indietro nel tempo. Ad esempio il positrone (che è l’antiparticella di un elettrone) invece di esser visto come un elettrone carico positivamente, può essere assimilato ad un elettrone che si muove indietro nel tempo. Ovviamente, poiché a livello macroscopico c’è un’evidente asimmetria tra passato e futuro, allora ciò implica che deve esistere almeno un evento, anche a livello microscopico, che sia asimmetrico rispetto al tempo, in modo tale che la il tratto infinitesimo di curva che abbiamo preso conservi anch’esso un residuo dell’asimmetria del tempo. Recentemente sono state osservate delle particelle (mesoni B) che rispetto all’inversione del tempo non si comportano in modo simmetrico.

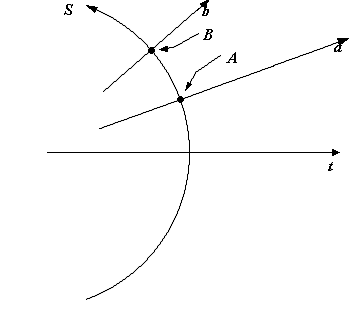
Notiamo inoltre un’altra cosa; affinché tutti gli osservatori vedano uno spazio-tempo omogeneo, è necessario che la linea di tempo di ogni osservatore sia sempre perpendicolare allo spazio. Questo implica che le linee di tempo dei vari osservatori non sono tra loro parallele. Questo discorso diventa più chiaro con i seguenti disegni:

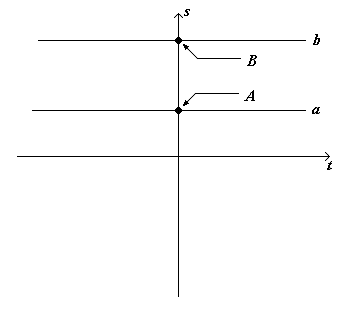
Nel disegno di sinistra abbiamo una rappresentazione classica di due osservatori, A e B che si trovano fermi nello spazio; le loro linee d’universo (le linee “a” e “b”) sono pertanto delle rette parallele all’asse del tempo. In tal caso, il tempo di A e il tempo di B sono fra loro paralleli. Ciò significa che il tempo misurato da A e il tempo misurato in B sono identici.

Nel disegno di destra invece le linee di tempo dei due osservatori (indicate sempre con “a” e “b”) sono perpendicolari all’arco della circonferenza e pertanto non risultano paralleli tra loro. Quando la distanza fra A e B è molto piccola, allora le loro linee di tempo risultano quasi parallele.

Se supponiamo che lo spazio-tempo sia come quello della figura di sinistra, allora per fare un confronto dei tempi, si prende un intervallo (ad esempio quello dell’osservatore A), lo si sposta verso l’alto in modo tale che esso continui a rimanere parallelo all’asse del tempo, finché non si sovrappone a quello di B. Giunto in questa posizione si esegue il confronto fra i due tempi. Invece, se supponiamo che lo spazio-tempo sia come nella figura di destra, per confrontare gli intervalli di tempo di A e di B, si deve eseguire una rotazione tale da mantenere l’intervallo in questione sempre perpendicolare all’arco di circonferenza che identifica la linea dello spazio. Per esempio, se vogliamo confrontare il tempo dell’osservatore A con quello dell’osservatore B dobbiamo immaginarci le linee di tempo come se fossero delle lancette di un orologio gigante; per confrontare il tempo di A con il tempo di B, dobbiamo far ruotare questa lancetta immaginaria fino a che non si sovrappone a B. In tal modo otteniamo un confronto corretto.

Se invece applichiamo il metodo della figura di sinistra, (avendo quindi fatto l’ipotesi sbagliata) allora ci accorgeremo che su distanze notevoli il modello di sinistra sbaglia, nel senso che ci descrive tempi sbagliati. Infatti questa cosa è vera a livello sperimentale. E’ noto che il confronto fra l’età degli oggetti che si trovano ai confini del nostro universo e l’età della terra, c’è una discrepanza notevole tale da aver seminato il dubbio sulla correttezza della teoria della relatività. Sperimentalmente si osserva che gli oggetti più lontani risulterebbero molto più giovani della terra.

La figura seguente illustra ancora meglio questo fatto. L’intervallo di tempo misurato dall’osservatore A è stato segnato sulla sua linea di tempo con il grigio chiaro. Sulla linea di tempo dell’osservatore B (e anche su C) è stato riportato con le due metodologie diverse. Nel primo caso eseguendo una rotazione si ottengono i tratti di tempo di B e di C; nel secondo caso, (metodo classico) si è effettuato uno spostamento parallelo all’ipotetico asse spaziale, mediante le linee tratteggiate. Quello che si ottiene in quest’ultimo caso sono gli intervalli di tempo “b” e “c”. Ora è possibile vedere che l’intervallo di tempo di un oggetto molto lontano risulta pertanto accorciato per un’errata interpretazione dello spazio-tempo. E’ possibile calcolare l’entità di curvatura dello spazio-tempo partendo proprio dall’errore che si commette nel confrontare l’età di un oggetto molto lontano con quella della terra. E’ ovvio che bisogna conoscere con esattezza la distanza dell’oggetto da noi e l’età stimata dell’oggetto.

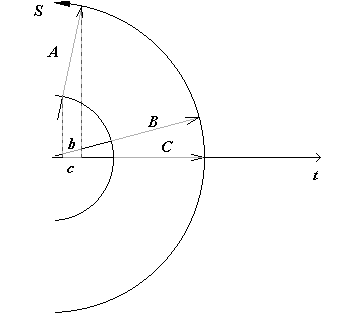
Prima di modellizzare lo spazio-tempo, facciamo un’ultima osservazione. Prendiamo lo spazio-tempo accelerato della figura seguente:

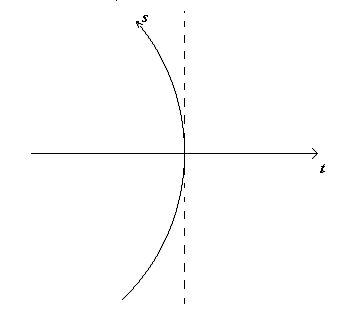
In questa rappresentazione abbiamo ovviamente omesso le altre dimensioni dello spazio; infatti il grafico riporta una dimensione dello spazio, più il tempo. E le altre due dimensioni spaziali?

Che fine hanno fatto? Bene, trattandosi di un piano, non potevamo ovviamente inserirle; però, poiché abbiamo a disposizione un’altra dimensione, che è quella uscente dal foglio, possiamo rappresentare due dimensioni spaziali in funzione del tempo. Una delle due dimensioni spaziali la chiameremo S_x e l’altra S_y. Sia l’una che l’altra dovranno avere lo stesso tipo di andamento nei confronti del tempo, ed inoltre dovranno essere fra loro ortogonali per omogeneità dello spazio. Queste condizioni portano alla figura seguente, dove si può facilmente notare che le curve S_x ed S_y generano una superficie curva; in particolare la superficie che viene a generarsi è la porzione di una superficie sferica.

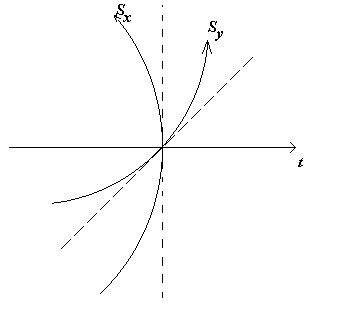
Per capire come essa si generi, basta immaginare che S_x ed S_y ruotino attorno all’asse t; quello che apparirà è proprio la porzione di una superficie sferica. Se ora generalizziamo, ci accorgiamo che se prendiamo una qualsiasi superficie nello spazio, essa deve risultare curvata rispetto al tempo in modo d’avere sempre una porzione di una sfera. E’ anche evidente dalla figura seguente, che le porzioni sferiche risultano sempre più grandi se vengono prese negli istanti di tempo successivi. Mano a mano che ci si allontana dal tempo di origine nel verso positivo del tempo, le superfici di spazio devono diventare sempre più grandi, mentre se guardiamo indietro le superfici sono più piccole.

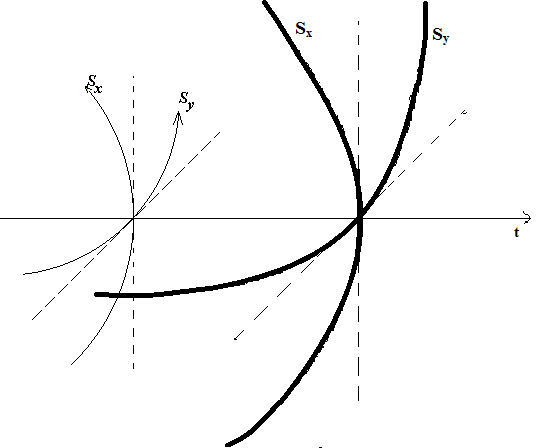
Ciò comporta che se vogliamo vedere una rappresentazione dello spazio in tutte e tre le sue dimensioni dobbiamo togliere la coordinata temporale e fare in modo che se prendiamo una qualsiasi superficie nello spazio, questa debba risultare appartenente ad una sfera. Questa condizione è soddisfatta se e soltanto se lo spazio (questa volta senza il tempo) risulta sferico. Infatti in questo modo, qualsiasi sia la superficie che prendiamo, risulterà per forza di forma sferica. Un’altra cosa importante che risalta agli occhi è che nel verso del tempo positivo, queste porzioni di superficie sferica tendono a diventare sempre più grandi, quindi nello spazio a tre dimensioni (che per semplicità chiameremo “universo”) avremo un’infinità di sfere sovrapposte in espansione; conseguenza immediata dello spazio-tempo accelerato è quindi l’universo in espansione, che risulta in perfetto accordo con le osservazioni sperimentali già condotte in astronomia. Quindi, l’universo è una sfera in espansione, però solo dal punto di vista spaziale. Questa osservazione però ci dice qualcosa di più rispetto a quello che ci dicono le osservazioni astronomiche. Infatti da queste sappiamo che tutti i corpi dell’universo sembrano essere in fuga gli uni rispetto agli altri come se fossero stati sparati da un punto di origine. Il ragionamento che abbiamo esposto supera questa visione e va ben oltre. Non è la materia ad essere proiettata da un punto d’origine, ma lo stesso spaziotempo. Anzi, c’è di più! Ogni punto dello spaziotempo si comporterebbe come una microsfera in espansione che si espande ad un ritmo ben preciso. Ciò implica che nel nostro universo ogni cosa si sta ingrandendo. Vi chiederete: “cosa? Ci stiamo gonfiando?” Esattamente! Se tutto si gonfia allo stesso ritmo non sarà possibile rendersene conto localmente. L’ingrandimento (su scala ridotta) è costante e pertanto non sarà possibile neanche notarlo. Invece su scale galattiche questo ingrandimento apparirà come se le stelle dell’universo fossero l’uvetta e i canditi di un panettone che sta lievitando, cioè sembrerà che si stiano allontanando come se ci fosse stato un big bang, ma in realtà quella potrebbe essere la vera freccia del tempo. Ogni istante è immortalato quindi da una precisa grandezza del guscio dello spaziotempo e da una precisa grandezza della materia. Ingrandire o rimpicciolire la materia potrebbe significare uno spostamento nel tempo. Detto questo, cerchiamo invece di ottenere la struttura dello spazio-tempo che sarà pertanto differente dalla forma dello spazio puro.

Per richiudere lo spazio tempo dobbiamo ricordarci due cose fondamentali: il fatto che lo spazio-tempo non è rappresentabile su un piano, ma su una superficie curva (con curvatura costante), e che lo spazio è curvo rispetto al tempo. Le superfici curve che soddisfano queste condizioni sono diverse; ad esempio le superfici sferiche e cilindriche sembrano entrambe soddisfare queste condizioni. Però notiamo che l’altra condizione (quella del dello spazio curvo rispetto al tempo) non può essere soddisfatta dalla superficie sferica; siamo quindi più propensi a pensare che la forma più adeguata allo spazio-tempo sia di forma cilindrica. Il lettore non faccia confusione tra il modello a sfere in espansione che abbiamo appena esposto, con quello che ora stiamo affrontando. Quello delle sfere in espansione lo abbiamo ottenuto escludendo il tempo e poi reintroducendolo come una serie di fotogrammi in sequenza (sfere via via sempre più grandi). Dal capitolo precedente abbiamo però ipotizzato che il tempo ha una struttura più complessa della semplice monodimensionalità, pertanto rappresentare uno spazio tempo a cinque o sei dimensioni può essere complicato. Al massimo possiamo escludere tre dimensioni e disegnare le restanti tre dimensioni. Ovviamente ogni volta verrà una rappresentazione che potrà essere differente dalle precedenti. Con tre dimensioni spaziali ed una temporale abbiamo trovato delle sfere in espansione. Proviamo ora ragionare in un altro modo e vediamo dove arriviamo. Prima di questa parentesi, stavamo dicendo che partendo dalla superficie di rappresentazione dello spaziotempo dovevamo usare una forma cilindrica. Quindi, dopo aver imposto la prima condizione abbiamo qualcosa che ha una forma simile alla figura seguente

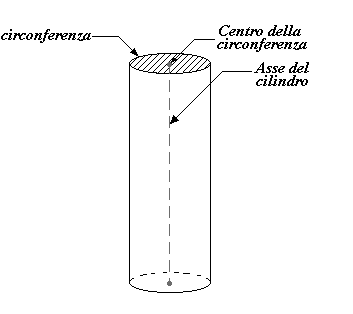
Tutti i percorsi paralleli all’asse del cilindro sono pertanto percorsi puramente spaziali, mentre tutti i percorsi circolari, concentrici alla circonferenza del cilindro, sono percorsi puramente temporali; tutti gli altri percorsi sono invece percorsi ibridi cioè spazio-temporali. Una cosa che bisogna subito notare è che i percorsi perpendicolari all’asse del cilindro (come il raggio della circonferenza) non sono né percorsi spaziali, né temporali, né tantomeno spazio-temporali. Questi percorsi non sono identificabili con nessuna delle dimensioni già conosciute, pertanto debbono essere percorsi appartenenti ad una dimensione d’ordine superiore alle quattro già conosciute, quindi potrebbe essere una delle due dimensioni non conosciute del tempo. Chiudiamo qui questa piccola parentesi e torniamo ad inserire un’altra cosa che avevamo dedotto; lo spazio è curvo rispetto al tempo. In tal caso il cilindro deve essere piegato in modo tale da rendere conto di questo fatto. Quello che otteniamo è quello che si vede nella figura seguente:

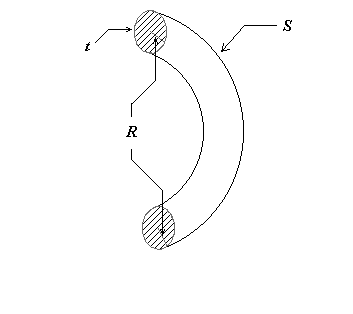
In questo disegno si è evidenziato che il cilindro è stato piegato per ottenere uno spazio curvo rispetto al tempo. Ora tutti i percorsi curvi come S sono percorsi spaziali, mentre quelli concentrici a t sono percorsi temporali; quelli indicati con la lettera R sono percorsi associati a questa quinta dimensione.

E’ da notare che questa struttura deve essere sempre la stessa indipendentemente dal lato dalla quale viene vista. Pertanto deve subire ancora un’altra distorsione tale da permetterci di avere un’omogeneità uniforme. Infatti se così non fosse si avrebbe l’assurdo di un tempo che si richiude su se stesso in una durata breve. Questo implica che ci deve essere una non perpendicolarità tra spazio e tempo. Questa mancanza di perpendicolarità porta la struttura di prima a non richiudersi ad anello ma a distorcersi leggermente fino a formare delle spire. Si arriva così al disegno successivo dove abbiamo rappresentato lo spazio-tempo nella sua forma più completa.

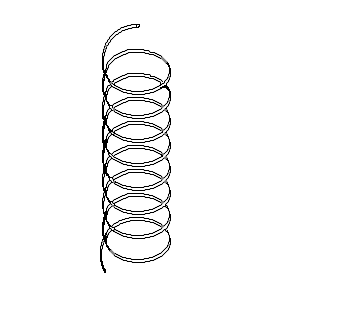
Il cilindro di prima deve pertanto avvolgersi su sé stesso più volte fino a formare una specie di molla. Ora, si può notare, che girando intorno alla molla, il suo aspetto è sempre lo stesso e che le sue curvature soddisfano ampiamente le richieste che avevamo imposto. La figura seguente dovrebbe essere più esplicativa nel singolo dettaglio.

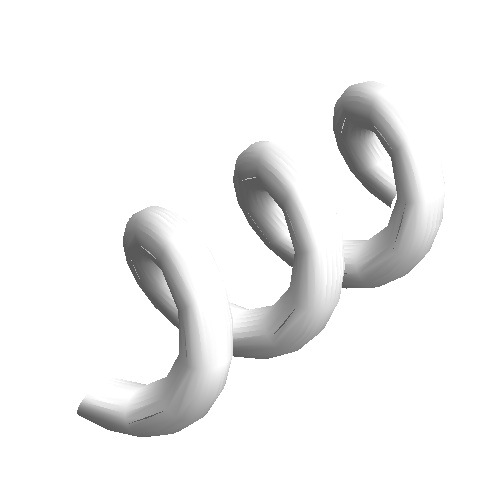
Ora il modello dello spazio-tempo è quasi completo, manca un solo dettaglio. Bisogna dire al nostro modello che lo spazio-tempo deve essere finito ma illimitato. Queste ultime due condizioni sono le condizioni che aveva imposto anche Einstein al suo modello per avere una rappresentazione coerente con le osservazioni sperimentali. Questa condizione ci obbliga a richiudere la struttura spiroidale su sé stessa fino a formare quella specie di ciambella come nella seguente figura.

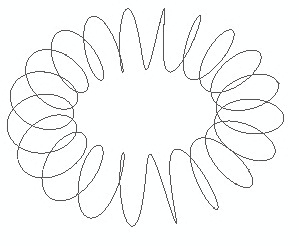
La figura a ciambella appena vista è la struttura dello spazio rispetto a due dimensioni del tempo, dove però abbiamo omesso lo spessore. Nella figura sembra essere molto sottile, anzi quasi filiforme, ma in realtà si tratta di un tubo cilindrico avvolto a spirale simile a quello della figura precedente. Da notare che lo stesso ragionamento può essere ripetuto su ciascuna dimensione spaziale insieme a due dimensioni temporali. In particolare ricordiamo come abbiamo costruito il grafico s-t, che per comodità riportiamo qui di seguito.

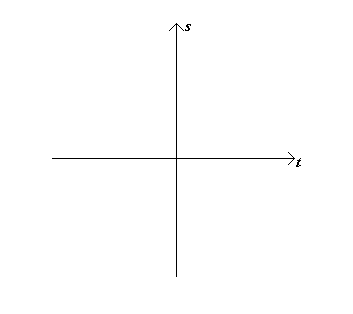
Avevamo preso l’asse x e lo avevamo assegnato al tempo, mentre l’asse y lo avevamo assegnato allo spazio. Implicitamente abbiamo detto che un’asse spaziale era ortogonale al sua corrispettiva dimensione temporale. Tecnicamente l’asse spaziale lo dovremmo chiamare S_x mentre quello temporale T_x, perché sono fra loro correlati. Analogamente per S_y e T_y, così come per S_z e T_z.

Avevamo anche fatto diversi ragionamenti che ci avevamo portato a dire che lo spazio doveva essere curvo rispetto al tempo. Ora in analogia possiamo dedurre che anche il tempo è curvo rispetto allo spazio con la concavità rivolta verso l’interno come nella figura seguente.

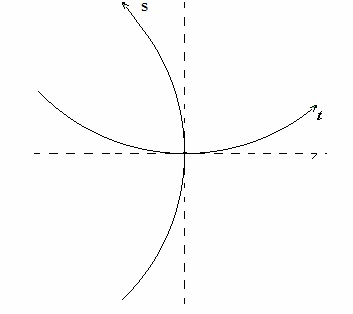
Ripetendo il ragionamento che avevamo fatto in precedenza arriviamo al grafico successivo, dove è possibile osservare che anche il tempo determina una porzione di una superficie sferica che si concatena allo spazio. Alla fine si può capire per analogia che anche il tempo si comporta come le sfere di spazio in espansione.

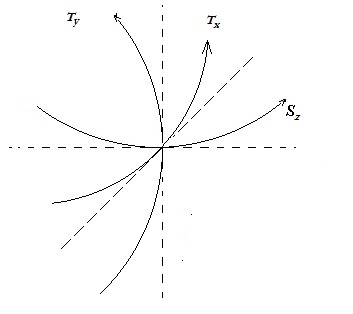
Questo è importante perché se lo spazio in espansione ci ha fatto capire che in passato eravamo fisicamente più “piccoli” di adesso, le sfere di tempo ci fanno capire che un intervallo di tempo del passato durava molto di meno di adesso. Ciò implicherebbe che il tempo sta rallentando. Pertanto le stime sull’età dell’universo potrebbero essere molto, ma molto più grandi di quanto non lo sia nella realtà. La datazione attuale è basata sul concetto matematico di “estrapolazione”[2]. Questa è un’operazione abbastanza nota nell’analisi numerica e spesso, nei libri di testo universitari, viene indicata come un’operazione potenzialmente azzardata, non priva di effetti collaterali. Ma facciamo una breve sintesi per i lettori meno eruditi in materia. L’interpolazione numerica è un’operazione che si esegue per calcolare una funzione matematica all’interno di un intervallo prefissato. In questo intervallo, vengono assegnati dei punti noti (detti nodi) dove la funzione assume valori notevoli. L’interpolazione permette di poter calcolare quella funzione all’interno di quell’intervallo ma in punti diversi da quelli conosciuti. Per fare questo si usano dei polinomi interpolatori che permettono di fare queste operazioni (dentro l’intervallo assegnato) e con un errore molto contenuto. Attenzione però ad applicare questi polinomi al di fuori dell’intervallo prefissato. E’ un’operazione pericolosa perché produce errori spaventosamente grandi. Questo vuol dire se l’intervallo di tempo entro cui è stata misurata una legge fisica è di un secolo, non è possibile estendere questa legge con assoluta certezza anche nei secoli più remoti. Nessuno ci garantisce che il tempo scorresse allo stesso modo. In altre parole, i miliardi di anni ipotizzati per il nostro universo, potrebbero essere in realtà solo diverse migliaia di anni. Ma c’è di più! Questo concatenarsi fra spazio e tempo ci fa venire in mente il concatenamento del campo elettrico con quello magnetico (che approfondiremo meglio nel prossimo capitolo) e che sta alla base della propagazione elettromagnetica. Verrebbe da pensare che una bolla di spazio genera una bolla di tempo che a sua volta genera un’altra di spazio e così via. La completa fusione di spazio e tempo (come la fusione di campo elettrico e magnetico) creerebbe il continum spaziotempo. Anzi a questo punto è possibile che la nostra bolla di spazio 3D si converta in una bolla di tempo 3D e che subito dopo si ritrasformi in una bolla di spazio 3D, analogamente a quanto accade alle onde elettromagnetiche dove il campo elettrico si trasforma in campo magnetico per poi riconvertirsi in campo elettrico e così via. Insomma, se le cose stessero in questo modo, verrebbe da pensare che il tempo non è quello che conosciamo.

[1] http://en.wikipedia.org/wiki/BOOMERanG_experiment

[2] http://it.wikipedia.org/wiki/Estrapolazione