Spazio Monodimensionale
Affrontare un discorso sulle dimensioni superiori può sembrare complicato, e in effetti potrebbe esserlo, per questo abbiamo ritenuto opportuno iniziare questo primo capitolo con degli esempi. Considerate uno spazio monodimensionale, cioè con una sola dimensione e immaginate che in esso vi sia un osservatore. Teniamo a precisare che in questa sede non ci interessa minimamente sapere come possa esistere un osservatore in un tale spazio, né tantomeno se possa vivere o come debba essere fatto il suo organismo. E’ invece importante sapere cosa “vede” all’interno del suo spazio ad una dimensione. Per fare questo vi invitiamo ad usare la vostra immaginazione. Supponete di trovarvi all’interno di un tunnel a sezione circolare e che, per una causa ignota, si stia restringendo.
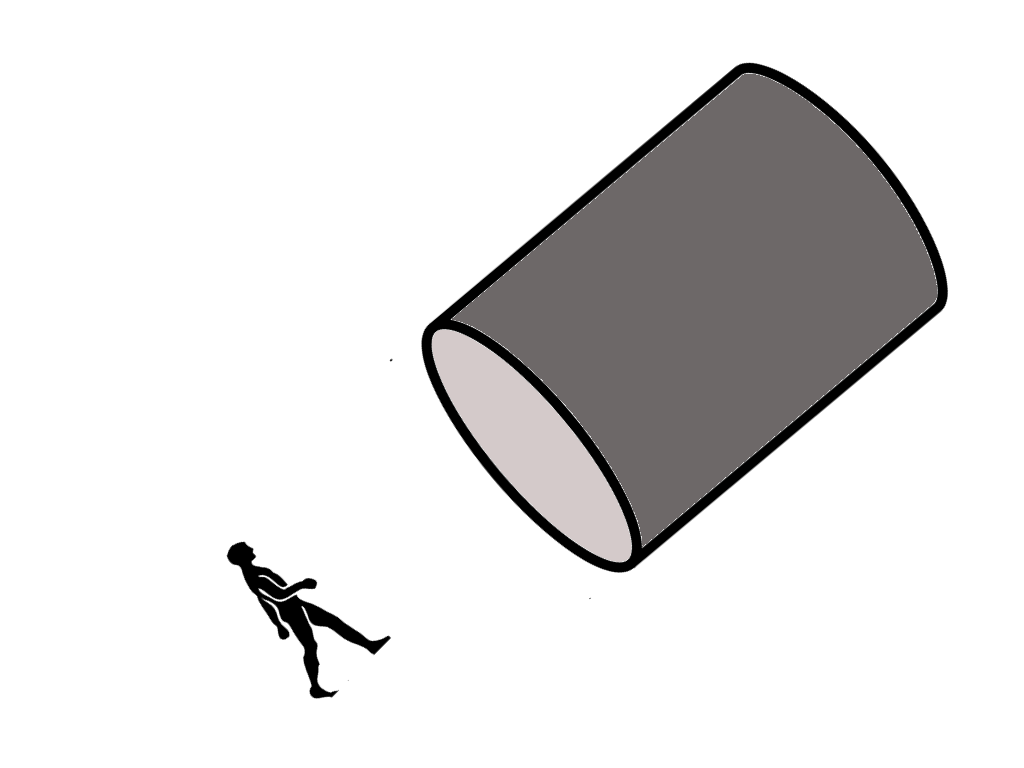
Ipotizzate che anche voi vi stiate rimpicciolendo in modo da non potervi accorgere di tale restringimento. Quando avrete spinto il ragionamento al limite, avrete come risultato finale che il tunnel sarà diventato una retta e voi sarete diventati un segmento. I vostri organi sensoriali (gli occhi per intenderci) non possono essere orientati in una dimensione perpendicolare alla retta perché, in uno spazio siffatto, le altre dimensioni non esistono. In altre parole non potete “guardare” ciò che è fuori dalla vostra retta, perché in uno spazio monodimensionale non esiste il “fuori dalla retta”; l’unica cosa che potete osservare è ciò che sta dentro. Questo significa che quello che stavate osservando, mentre il tunnel si stava restringendo, era il fondo del tunnel stesso. Pertanto all’inizio vedevate un “cerchio”, che per effetto del restringimento si sarà rimpicciolito, fino a diventare un punto.

Da questo ragionamento possiamo quindi dedurre che il nostro osservatore vede un punto. Inoltre, non può muoversi (non ha la dimensione del tempo che glielo permette di fare), e ciò significa che lui ha un’immagine statica di fronte a sé che gli rimane invariata. Si noti che se avessimo ipotizzato lo scorrimento del tempo, le dimensioni in gioco sarebbero state due anziché una. Invece, per ora, è importante escludere il tempo dai questi ragionamenti. Abbiamo così dedotto che un osservatore a “dimensione uno” (cioè un segmento), vede gli oggetti di fronte a sé come se fossero a dimensione zero (un punto).
Spazio Bidimensionale
Andiamo avanti e proviamo a considerare un osservatore che si trovi all’interno di uno spazio bidimensionale, cioè a due dimensioni. Come nel caso precedente, vogliamo capire cosa “vede”. Per fare questo, vi proponiamo questo ragionamento. Supponete di trovarvi all’interno di un salone e che per una ragione sconosciuta il soffitto si stia abbassando. Ipotizzate che anche voi vi stiate abbassando insieme al soffitto in modo da non rendervi conto di tale fenomeno. Se spingete il ragionamento al limite, il salone sarà diventato un piano e voi una generica figura contenuta nel piano stesso. I vostri organi sensoriali, non possono puntare verso l’alto, perché in questo spazio, la dimensione perpendicolare al piano non esiste. Quindi “gli occhi” del nostro ipotetico osservatore debbono per forza guardare in una direzione giacente nel piano. Ribadiamo che il nostro ipotetico “omino”, sarà diventato una figura geometrica chiusa, giacente all’interno del piano stesso, come ad esempio un cerchio, un quadrato o una figura piana qualsiasi.
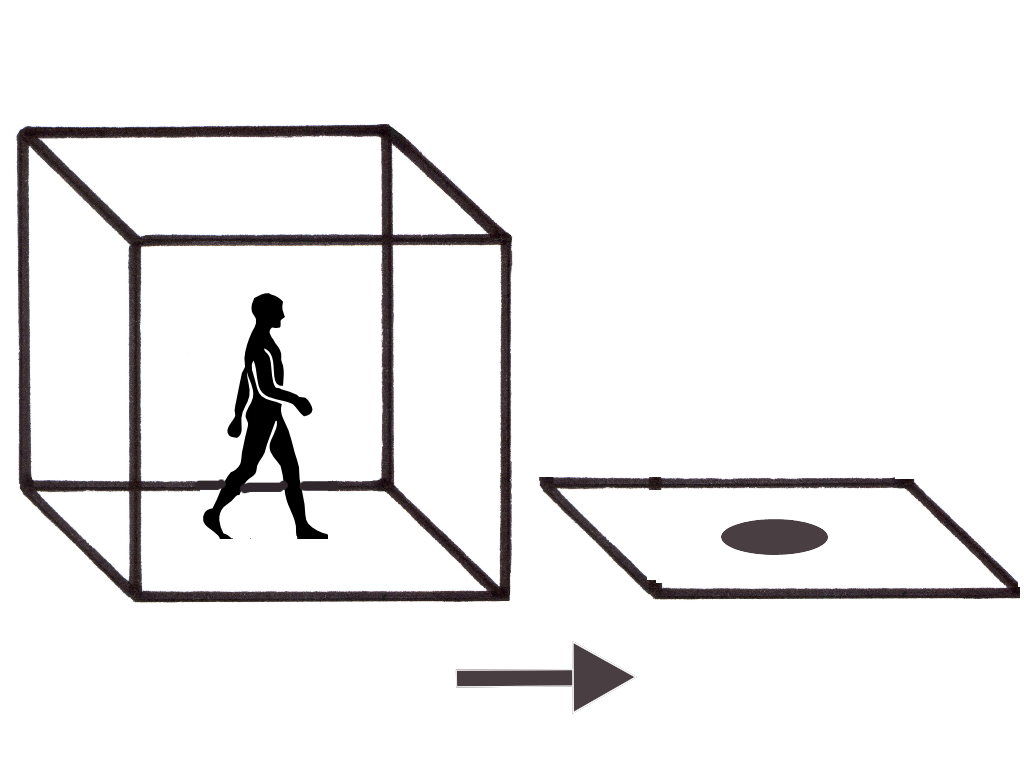
Ora cerchiamo di capire cosa osserva. Per fare
questo ritornate con la mente al momento in cui il salone si stava abbassando.
Se stavate guardando un tavolo, vedrete quest’ultimo che s’abbassa sempre di
più, fino a diventare molto sottile, cioè in ultima analisi, un segmento.
Quindi, tutti gli oggetti da lui osservati sono segmenti, più o meno lunghi.
Anche quest’osservatore come il precedente non può muoversi, perché anche lui
non ha a disposizione la dimensione tempo. Anche lui avrà un immagine statica
di fronte a sé; nel suo caso però vedrà dei segmenti immobili. Con questo ragionamento, abbiamo dedotto che
un osservatore a “dimensione due” (figura piana), vede oggetti a “dimensione
uno” (segmenti).
Spazio Tridimensionale
Proseguiamo il nostro ragionamento considerando un osservatore che si trovi all’interno di uno spazio tridimensionale. Anche questa volta vogliamo capire cosa “vede”. Questa volta è molto più semplice. Supponete infatti, che quest’osservatore si trovi all’interno del salone di cui parlavamo prima. Immaginate che stia osservando una parete. Quello che vede di fronte a se è un piano. Anche quest’osservatore, come i precedenti non ha a disposizione la dimensione tempo, per cui non si può muovere e vedrà di fronte a se un piano statico, in cui non c’è movimento.
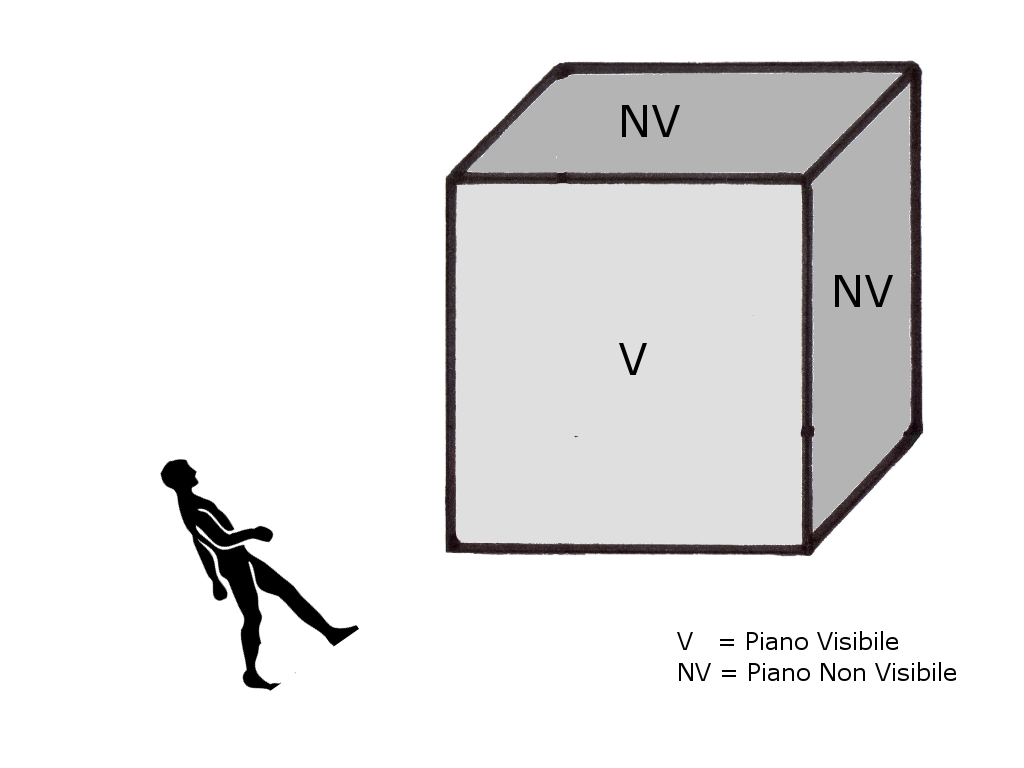
Se avete qualche dubbio a tal riguardo, provate ad immaginare la seguente situazione. Pensate di avere di fronte a voi una grande parete sulla quale ci sono due finestre che distano fra loro cinque metri. Supponete di trovarvi ad una decina di metri dalla parete e che potete guardare agevolmente le due finestre. Dietro una delle due, ad un paio di metri circa, c’è una foto gigante che raffigura un panorama, mentre dietro l’altra c’è lo stesso panorama, ma reale. Se sulla foto non ci sono riflessi di luce, e se voi non vi muovete, sarà difficile, se non impossibile, stabilire in pochi secondi qual è il vero panorama e qual è la foto. Questo fatto dovrebbe convincervi a sufficienza che se non c’è movimento, non si percepiscono tre dimensioni ma due. Quindi, abbiamo dedotto che un osservatore a “dimensione tre” (corpo solido), vede oggetti a “dimensione due” (piani).
Spazio Quadrimensionale
Consideriamo un osservatore che si trova all’interno di uno spazio quadrimensionale. Quest’osservatore può essere uno di noi. Egli infatti, ha a disposizione come noi tre dimensioni dello spazio più quella del tempo. Il fatto di avere a disposizione il tempo gli consente di muoversi, per cui “vede” una successione di spazi bidimensionali che gli permette di ricostruire nella propria mente le tre dimensioni.
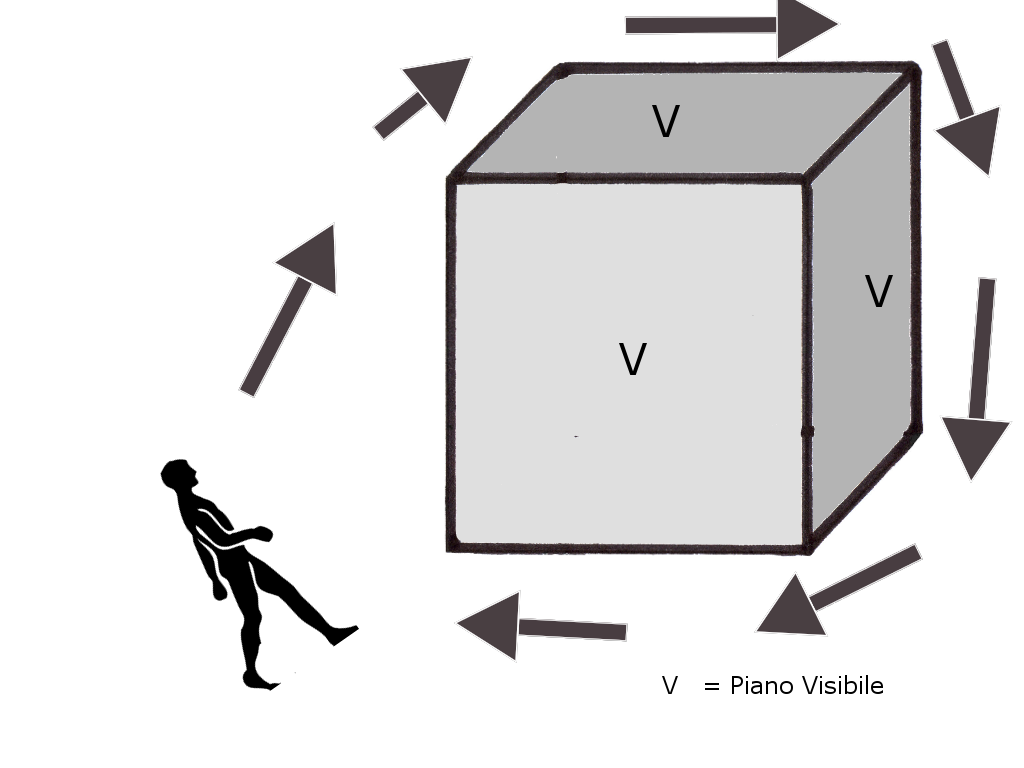
Nuovamente abbiamo capito che un osservatore a “dimensione quattro”, vede oggetti a “dimensione tre” (oggetti solidi).
Teorema sulla vista
Se ora riepiloghiamo i risultati, otteniamo una conclusione non banale. Avevamo visto che l’osservatore a “dimensione uno” vedeva oggetti a “dimensione zero”. Con ragionamenti simili, eravamo arrivati a capire che l’osservatore a “dimensione due” vedeva oggetti a “dimensione uno”. Proseguendo nella nostra analisi abbiamo concluso che l’osservatore a “dimensione tre” vedeva oggetti a “dimensione due”. Infine abbiamo visto che l’osservatore a “dimensione quattro” vedeva oggetti a “dimensione tre”. La tabella seguente riepiloga sinteticamente ciò che è stato detto.
| Dimensioni Reali | Dimensioni Osservate |
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
Guardando questa tabella, capiamo che nell’osservare gli oggetti del proprio spazio, un qualsiasi osservatore perde una dimensione. Possiamo generalizzare il tutto dicendo che l’osservatore di uno spazio ad “n” dimensioni, osserva oggetti a dimensione “n-1”, dove con la lettera “n” abbiamo indicato un generico numero intero positivo. Pertanto, per fissare meglio le idee, questo vuol dire che “n” può valere 1, o 2, o anche 3, oppure 4, o anche 5 e così via fino a numeri grandi a piacere, ma comunque interi positivi.
E’ facile giungere anche alla seguente deduzione: un osservatore di uno spazio ad “n” dimensioni, non può vedere oggetti appartenenti a dimensioni superiori. Ciò è evidente se si ripercorre tutto l’iter che ci ha portato dalla prima fino alla quarta dimensione. L’osservatore della prima dimensione non riesce a vedere oggetti appartenenti alla seconda, alla terza o alla quarta dimensione, a meno che questi non gli vengano interposti sul suo “cammino d’osservazione”, cioè all’interno della sua retta; ma nonostante ciò li vedrebbe comunque come dei punti. Analogamente l’osservatore della seconda dimensione, non riesce a “vedere” oggetti appartenenti alla terza o alla quarta dimensione, a meno che questi non vadano ad intersecare il suo piano; in tal caso li vedrebbe comunque come segmenti. Similmente l’osservatore della terza dimensione non riesce a vedere quello della quarta, a meno che questo non gli si ponga davanti, in modo stabile, sul suo “cammino d’osservazione”; in tal caso vedrebbe gli oggetti dello spazio a quattro dimensioni come bidimensionali. Più in generale possiamo dire che: se un osservatore, appartenente ad uno spazio ad “n” dimensioni riesce a “vedere” gli oggetti appartenenti ad uno spazio a dimensioni superiori, allora li vede come oggetti del proprio spazio, vale a dire con “n-1” dimensioni. Questo fatto è importante perché ci dice che se degli oggetti a 5, a 6 o più dimensioni entrassero nel nostro spazio, noi non saremmo capaci di percepirne le loro dimensioni extra, ma li vedremmo comunque come oggetti del nostro mondo. Probabilmente presenterebbero delle proprietà fisiche curiose, come apparire simultaneamente in due posti diversi, o comunicazioni istantanee a distanza enorme o chissà cos’altro; ma a parte questo non noteremmo nient’altro di strano.
E’ quindi una conseguenza di tutto ciò che: un osservatore di uno spazio ad “n” dimensioni, può vedere tutti gli osservatori che si trovano negli spazi ad “n-1”, “n-2” etc. …”3”, “2”, “1” dimensioni, ma, salvo casi particolari, non può accadere il contrario; inoltre tutti gli osservatori dei sottospazi di “n”, sono visti dall’osservatore dello spazio ad “n” dimensioni come se fossero di dimensione “n-1”.
Questa definizione è in altre parole una “regola per le dimensioni” o “Teorema Della Vista” (vedi Capitolo allegati per una dimostrazione matematica).
Quindi, ad esempio, un osservatore della quarta dimensione può gironzolare intorno ad un osservatore della terza senza che lui se ne renda conto; non potrà vederlo, fin quando non gli si pone di fronte e rimane immobile per un tempo infinitamente lungo. Però il fatto che l’osservatore della terza dimensione non vede quello della quarta, non implica che quello della quarta non esiste; tutt’altro non solo esiste, ma avendo una dimensione in più può fare cose che a quello della terza non sono permesse: può muoversi!
E’ facile convincersi che
gli osservatori dei sottospazi siano visti dall’osservatore di dimensione “n”
come appartenenti al suo spazio, cioè ad “n-1” dimensione. Ad esempio,
l’osservatore monodimensionale sarà visto come tridimensionale dall’osservatore
a quattro dimensioni. L’osservatore a quattro
dimensioni vedrà anche lo spessore e la larghezza dell’osservatore
monodimensionale, ed affermerà che queste dimensioni sono molto piccole, ma non
trascurabili. Analogamente, vedendo un osservatore bidimensionale, affermerà
che lo spessore del piano, su cui si trova l’osservatore bidimensionale è
piccolissimo, ma non è zero. In altre parole, l’osservatore di uno spazio ad “n”
dimensioni, riconduce tutti gli oggetti da lui osservati ad “n-1” dimensioni.
Analogamente se il nostro mondo fosse a 5 o 6 o più dimensioni, noi potremmo
già possedere queste dimensioni extra, ma se avessimo uno “spessore” molto
piccolo rispetto a queste dimensioni superiori ed inoltre fossimo vincolati
rispetto ad esse, potremmo trovarci nella condizione di non avere libertà di
movimento rispetto a queste dimensioni e quindi ci sembrerà che queste
dimensioni non esistano. Al contrario un osservatore che possedesse la libertà
di movimento rispetto a queste dimensioni extra, vedrebbe che noi siamo già in
una condizione di completezza rispetto a queste dimensioni, ma analogamente
direbbe che il nostro spessore e i vincoli dimensionali ci permettono di avere
solo la libertà di movimento nelle dimensioni spaziali. Pertanto
quest’osservatore concluderebbe il suo intervento dicendo che la nostra
situazione ci può indurre ad avere una falsa sensazione di un mondo a 3
dimensioni spaziali più una temporale.
Un Piccolo Esempio
Torniamo ora a discutere l’ipotesi delle superstringhe che avevamo preso nell’introduzione del libro e cioè delle dimensioni “arrotolate nell’infinitamente piccolo” e verifichiamo che questa idea contiene un errore di valutazione. Per fare questo ci aiutiamo con il seguente esperimento mentale. Immaginate un osservatore a tre dimensioni (due per lo spazio e una per il tempo) che vive tranquillamente nel suo mondo piano. Pensate inoltre che la superficie su cui esso si muova sia la superficie di un lago.

Ora, servendoci dell’immaginazione, proviamo a pensare di immergere un pallone dentro l’acqua del lago, in modo che questo strano osservatore possa vederlo. Egli vedrà apparire dal nulla un punto, che via, via gli si aprirà davanti per diventare un segmento, per poi restringersi di nuovo in un punto che a sua volta sparisce di nuovo nel nulla. Pertanto, dalla sua visuale, tutto appare “come se”, in un punto ben preciso del suo piano, ci siano delle “dimensioni arrotolate” da cui fuoriesce quest’oggetto misterioso. Un’altra interpretazione che potrebbe usare, se pensiamo al concetto di prospettiva, è che il punto che gli è comparso davanti sia in realtà un cerchio molto lontano in progressivo avvicinamento. Infatti quando lo vede ingrandirsi, la sua esperienza quotidiana lo porterà a pensare che si tratta di un cerchio molto lontano che lentamente si sta avvicinando a lui. Viceversa, quando lo vede rimpicciolirsi, penserà che il cerchio si stia allontanando di nuovo, fino a sparire dalla sua vista. In questo caso non penserà ad un fenomeno insolito se nel luogo dove avviene questo “incontro” c’è uno spazio libero sufficiente per fargli credere che ci sono stati questi spostamenti. Però se dietro il cerchio ci fosse un ostacolo che impedisse l’avvicinamento, non potrebbe pensare che il cerchio si sia avvicinato passando attraverso un ostacolo, ma a quel punto sarebbe portato a pensare alle dimensioni arrotolate. In realtà, egli non sa che le dimensioni non sono affatto arrotolate, ma che la sua prospettiva limitata lo induce a credere a questo fatto. Per analogia, possiamo capire che se dovessero esistere delle dimensioni superiori alle nostre, queste non potrebbero essere arrotolate… il fatto che non le vediamo significa soltanto che la nostra struttura a quattro dimensioni ci impedisce di poter gettare il nostro sguardo verso le altre dimensioni, cioè ci troveremmo nella stessa situazione in cui era l’osservatore dell’esperimento precedente, cioè che non poteva alzare lo sguardo verso l’alto perché quella dimensione gli era preclusa dalla sua conformazione e dai vincoli del suo spazio.
Alla luce di questi fatti, è facile capire che la costruzione di una teoria basata sul concetto di dimensioni arrotolate, può apparire come una falsificazione della realtà. Ma allora perché si parla tanto di queste teorie? Il problema nasce dal fatto che sempre più matematici si occupano di fisica e che i fisici a loro volta si sono trasformati in matematici. Quando un matematico applica i suoi ragionamenti alla fisica, non si preoccupa molto dell’aspetto fisico-filosofico, ma soltanto di quello matematico. Spesso accade che per il solo fatto di aver applicato tutta quella matematica sofisticata, i loro ragionamenti siano presi seriamente in considerazione. Se poi, per pura coincidenza, riescono a dimostrare qualcosa di nuovo è la fine! Da quel momento quelle teorie diventano il nuovo “vangelo” della fisica, fino a quando qualcuno non le mette seriamente in discussione. Noi rivendichiamo la supremazia della fisica sulla matematica; la matematica è solo uno strumento della fisica, (o dell’ingegneria), ma non è la “via maestra” per scoprire cose nuove. Senza un solido ragionamento non si va da nessuna parte ed Einstein, con la sua relatività, ce lo dimostrò ampiamente. Il suo capolavoro non fu quello di introdurre l’algebra tensoriale per la sua teoria, ma di capire che se un corpo si avvicina alla velocità della luce, intorno a questo si distorcono lo spazio e il tempo. Poi con ulteriori osservazioni brillanti, capì che se la velocità ha un effetto simile, a maggior ragione farà l’accelerazione. La vera ciliegina sulla torta fu il passo finale, cioè quello di capire che accelerazione e gravità sono equivalenti e quindi che a sua volta la gravità distorce lo spaziotempo. Senza queste disquisizioni fisiche-filosofiche, il resto della sua teoria non poteva essere costruito. Queste sono state le solide fondamenta e l’ossatura portante della teoria della Relatività Generale[1]. Una volta imboccata la strada giusta, il resto della teoria è solo una lunga serie di esercizi matematici più o meno complicati.
La Quinta e la sesta dimensione
Parlare di una quinta dimensione non è facile, anche perché a mala pena sappiamo come sono fatte le altre quattro, ma il teorema della vista che abbiamo appena introdotto può venirci in aiuto. Prima di andare oltre, notiamo una cosa singolare. Lo spazio ha 3 dimensioni, mentre il tempo sembra averne una sola. La natura, sotto molti aspetti, ci ha abituati a vedere molti fenomeni con delle eleganti simmetrie. Si pensi alle cariche positive e negative, al polo nord e al polo sud magnetici, e a molti altri aspetti che sia a livello microscopico che macroscopico riflettono queste simmetrie. Ora proprio in virtù della simmetria, sarebbe stato più armonioso avere un tempo a tre dimensioni; invece ne abbiamo solo una. In tal caso avremmo avuto 3 dimensioni per lo spazio e 3 dimensioni per il tempo. E se le cose stessero in modo differente, noi ce ne potremmo accorgere? Il Teorema della Vista che abbiamo appena esposto ci direbbe di no, ma per capire meglio questo fatto, facciamo un esempio ipotetico. Prendiamo dei tubicini di vetro e li colleghiamo fra loro in modo da formare un albero, con biforcazioni e ramificazioni multiple. Inseriamo dentro un bruco dello stesso diametro del tubo, in modo che possa scorrere dentro con agevolezza, ma non possa girarsi ne a destra, ne a sinistra, ne sopra e ne sotto; può solo andare avanti.
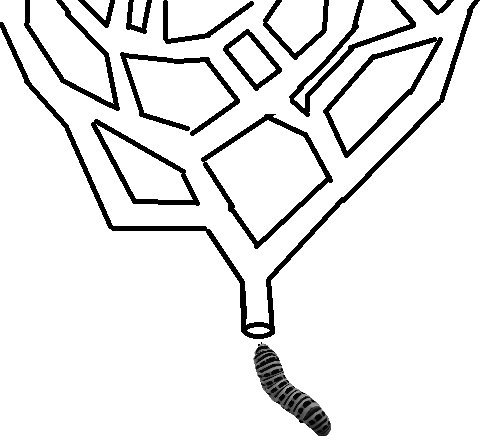
Una volta che avrà iniziato il suo cammino, arriverà alla prima biforcazione e potrà “scegliere” se imboccare il canale alla sua sinistra o alla sua destra. Una volta però entrato, non potrà più tornare indietro. Successivamente, dopo aver percorso un altro tratto senza ramificazioni si troverà di fronte ad un’altra ramificazione con 2 o più percorsi a sua scelta. Una volta sceltone uno, continuerà in quella direzione senza tornare indietro. Per le sue piccole dimensioni, e per come sono fatti i tubi, il bruco si comporterà come un osservatore monodimensionale. Avrà però di tanto in tanto la possibilità di scegliere dove andare. Maggiori ramificazioni incontrerà di fronte a sé, maggior possibilità di scelta avrà a sua disposizione. Il bruco si troverà più o meno nella stessa condizione di un osservatore monodimensionale, anche se di fatto si trova in uno spazio a tre dimensioni. Queste ramificazioni che lui si trova di fronte, non le interpreterà come la presenza di ulteriori dimensioni, ma come una naturale conseguenza del suo spazio monodimensionale. Non potendosi girare in nessuna direzione, non avrà acquisito la capacità di prendere coscienza delle altre due dimensioni e accetterà queste ramificazioni, come uno stato naturale del suo spazio monodimensionale. Non penserà affatto che ogni qualvolta lui ha una possibilità di scegliere strade diverse, queste rappresentino la prova cruciale dell’esistenza di altre dimensioni spaziali. Anzi, se vivesse in un mondo fatto in quel modo, dove altri bruchi più anziani gli hanno insegnato che le diverse gallerie, non sono altro che le varie opzioni di scelta, non si fermerà mai a pensare in un modo diverso. Se la natura induce a credere una determinata cosa ad un gruppo folto di persone, è difficile poi andare a sradicare quella convinzione (si pensi alla concezione di Terra piatta prima della scoperta dell’America, alla teoria geocentrica prima della dimostrazione di quella eliocentrica, ecc.).
Proviamo ora a spostare questo esempio sul tempo. E se il tempo avesse un comportamento simile? Se il tempo fosse tridimensionale, ma per un qualche motivo oscuro ci trovassimo nella stessa situazione del bruco, noi ce ne potremmo accorgere? La risposta non è così facile ed immediata. Non potremmo dire subito si, ma allo stesso modo non potremmo nemmeno scartare questa ipotesi. Dopotutto una curva generica nello spazio a tre dimensioni può essere ricondotta alle sue componenti fondamentali, lunghezza, larghezza ed altezza; ciononostante il tragitto su questa curva, per l’osservatore monodimensionale che la percorre, non sarà differente da una qualsiasi linea dello spazio, cioè sarà sempre e comunque monodimensionale. Pertanto anche il tempo che noi consideriamo come dimensione unica, potrebbe essere più complesso di quello che sembra. Potrebbe essere una curva generica in un tempo 3D; ma dal nostro punto di vista, essendo bloccati in questa curva, il tempo ci apparirebbe sempre e comunque monodimensionale. Forse, solo a livello microscopico le cose potrebbero cambiare. Infatti, il tubicino in cui cammina il bruco ha delle pareti dritte, rigide e perfettamente levigate, pertanto non presenta delle increspature che gli facciano sospettare la presenza di un’altra dimensione. Se però guardassimo con un potentissimo microscopio quelle pareti, noteremmo che non sono veramente lisce come sembrano, ma che presentano delle increspature, degli avvallamenti che tradiscono la presenza di un’altra dimensione spaziale. Il bruco però, da parte sua, non ha la sensibilità di percepire queste imperfezioni sulla superficie e pertanto non si ferma a pensare a questi fatti. Spostando di nuovo questo ragionamento sul tempo, possiamo capire che a livello microscopico il tempo che noi supponiamo monodimensionale, potrebbe presentare delle imperfezioni che tradiscono la presenza delle altre due dimensioni temporali. Ovviamente, queste “imperfezioni” possono agire solo a livello microscopico, dando alla materia delle proprietà speciali. Vedremo in seguito, nel capitolo Luce e Materia, come il paradosso EPR[2] possa legarsi al concetto di tempo tridimensionale e come certi aspetti misteriosi del mondo dei quanti trovino una collocazione razionale nel contesto di un tempo 3D. Questo fatto poi, non è così strano come sembra. Anche nella fisica teorica di frontiera, quella che cerca nuove teorie o cerca di metterle alla prove ipotizza esistenza di altre dimensioni, si fa qualcosa di simile. Ne sono un esempio la teoria delle stringhe, e la successiva evoluzione verso la teoria M. Alcuni ricercatori, ad esempio, hanno provato ad eseguire un’estensione della teoria della relatività generale a più di 4 dimensioni. Tali estensioni della relatività seguono il filone di ricerca aperto dai matematici Theodor Kaluza e Oskar Klein che introdussero rispettivamente altre dimensioni e il concetto di compattificazione delle dimensioni extra. Ad esempio, il ricercatore Xiaodong Chen, ha pubblicato su Arxiv.org[3] una interessante elaborazione della teoria della relatività a 6 dimensioni (tre spaziali e 3 temporali). La cosa interessante del suo lavoro è che, l’equazione del moto di una particella in uno spazio tempo 6D, assuma la forma di una funzione d’onda identica a quella della meccanica quantistica. Quindi, senza invocare nessun principio di indeterminazione, il Dott. Chen ha scoperto che è sufficiente ipotizzare un tempo 3D per ricavare molte delle proprietà della meccanica quantistica. Questa parentesi era d’obbligo per far comprendere al lettore che un tempo 3D è più naturale di quanto non possa sembrare. E’ probabile che solo nel mondo infinitamente piccolo emerga la natura 3D del tempo e che nel mondo macroscopico questa natura scompaia per dare posto ad un tempo che sembra solo monodimensionale., ragion per cui nel mondo macroscopico non notiamo nessuna delle bizzarre conseguenze della meccanica quantistica.
Chiusa questa parentesi, vogliamo sottolineare che, se le cose stessero davvero così, tutto avrebbe un senso logico diverso. Anzi, ci verrebbe da dire che se il tempo fosse ad una sola dimensione noi non potremmo esistere. Ad ogni istante della nostra vita abbiamo la chiara percezione che possiamo “scegliere” cosa fare. In qualsiasi istante possiamo decidere se pensare, se sederci, se alzarci, se sdraiarci, se parlare, se cantare, se saltellare, se correre, se dormire e così via con tutte le azioni possibili ed immaginabili che vi vengono in mente. Ad ogni istante noi possiamo arbitrariamente cambiare quello che stavamo facendo in un qualcos’altro. Vi chiederete cosa c’entrano queste scelte con il tempo tridimensionale. Se il tempo fosse governato da una sola dimensione temporale, il caos del mondo microscopico non avrebbe ragione d’esistere. L’universo, con una sola dimensione temporale, sarebbe esattamente come la visione di Newton, cioè predeterminato. Sarebbero come le biglie di un biliardo che una volta colpite si muoveranno secondo uno schema fisico ben preciso, prestabilito dal colpo iniziale. Ogni cosa accadrebbe perché deve accadere, come se fosse una specie di destino già scritto. Ma l’esperienza quotidiana ci insegna che le cose non stanno così. Possiamo di volta in volta scegliere cosa fare o cosa non fare, cosa dire o cosa non dire, è molto di più che una semplice sensazione è la realtà fisica dei fatti. Questa nostra “capacità” di scelta, potrebbe celare la presenza di ramificazioni nella nostra linea di tempo. D’altra parte il caos del mondo microscopico e l’impossibilità di applicare la fisica di Newton al mondo dell’infinitamente piccolo, ci dovrebbero far sorgere qualche sospetto sul presunto concetto di tempo monodimensionale che ci hanno inculcato nelle scuole e nelle università. Abbiamo accennato alla possibilità che eventuali increspature in un tempo 3D possano svelarsi nel mondo subatomico. Ora va detto che la fisica dei quanti, che studia i fenomeni nel mondo microscopico, da parte sua introduce dei concetti matematici astrusi che fanno riferimento ad un’algebra ad infinite dimensioni (anche se lo stesso Heisenberg ci tiene a precisare che si tratta di dimensioni astratte). Questa necessità di richiamarsi ad infinite dimensioni (anche se astratte) dovrebbe accendere in noi un ulteriore campanello d’allarme che forse il tempo 3D potrebbe essere una possibile chiave di lettura di certi fenomeni.
D’altro canto la nostra visione del tempo alcune volte ci dà la possibilità di anticipare gli eventi. Quante volte, abbiamo sentito dire: “me lo sentivo che sarebbe andata così”. Altre volte sentiamo racconti di persone che nei sogni dicono di aver visto eventi futuri che poi si sono avverati. Ed ancora, quante volte si sente parlare di deja-vu[4]? Il teorema della vista parla chiaro. Se apriamo la strada ad una quinta o ad una sesta dimensione temporale, aumenta la visibilità che ha l’osservatore. In questo caso si parlerebbe di visibilità di eventi futuri o eventi passati. Ovviamente vedere eventi passati, non ci entusiasma molto, per quello c’è già la nostra memoria che ci dà visibilità sul nostro passato, ma se vedessimo eventi passati che si riferiscono ad un tempo antecedente alla nostra vita attuale sarebbe tutt’altra cosa. Viceversa la visione del futuro è quella che ci stimola di più, ma d’altra parte ci inquieta anche un po’. Queste cose di cui sentiamo ogni tanto parlare, potrebbero avere una spiegazione scientifica seria legata alla tridimensionalità del tempo. Questi eventi, apparentemente strani ed inspiegabili, acquisterebbero un senso logico diverso se il tempo fosse davvero 3D. Delle increspature occasionali nella nostra linea di tempo potrebbero permettere queste stranezze, facendoci acquisire in modo estemporaneo la capacità di sbirciare più avanti lungo la linea temporale. Questo accadrebbe perché in quel caso saremmo fuoriusciti dalla nostra linea di tempo di quel tanto che basta da permetterci di sbirciare più avanti lungo la linea temporale su cui ci trovavamo, ma non così tanto da farci sparire dalla linea di tempo stessa. Detto questo, ci interessa sottolineare che sebbene tutto ciò abbia un senso logico, ci sarebbero notevoli difficoltà tecniche per riprodurre sperimentalmente tali fenomeni, ma non per questo intendiamo scoraggiarci.
Se questi ragionamenti fossero corretti, allora potremmo classificare le dimensioni in un modo diverso. Le prime tre, le classificheremmo sotto il nome “classe spazio”. Le altre tre, per analogia, assegneremmo la denominazione di “classe tempo”. E’ interessante osservare, che l’introduzione di una nuova classe, “attiva” delle possibilità dell’osservatore. La sola classe spazio, non permette di fare nulla al nostro osservatore. Non appena introduciamo una dimensione della classe tempo, gli consentiamo di muoversi… ma solo a velocità costante; infatti la velocità è il rapporto tra lo spazio percorso e il tempo impiegato, cioè “una sola dimensione del tempo”. Nel momento in cui introduciamo una ulteriore dimensione temporale, diamo la possibilità di avere un’accelerazione, ma localmente non vedremmo nessuna differenza. Infatti, da un punto di vista strettamente matematico, l’accelerazione è il rapporto fra la velocità e il tempo, oppure il rapporto fra lo spazio e il “quadrato del tempo”. A tal proposito raccontiamo un aneddoto capitato a Fabio. Discutendo anni fa con un suo cugino ingegnere civile, veniva invitato a riflettere sui significati di certe grandezze fisiche all’interno di formule matematiche. Il cugino ingegnere invitava Fabio a cogliere anche il significato filosofico che si potrebbe assegnare a certe grandezze, come ad esempio il “quadrato del tempo”. Mentre se in una formula fisica o ingegneristica compaiono i “metri quadri”, sappiamo di cosa stiamo parlando, perché il metro quadro lo possiamo vedere e sappiamo che stiamo parlando di un’area, la stessa cosa non si può dire per il “tempo quadro”. Al di là, del risultato a cui conduce ogni singola formula, non sappiamo assegnare un vero significato fisico al tempo quadro. Lo sappiamo solo se lo leghiamo ad un’altra grandezza fisica, come lo spazio, ottenendo ad esempio un’accelerazione, ma se il “tempo quadro” è preso da solo, non sappiamo dargli un senso fisico. Ora invece, alla luce di queste osservazioni, potremmo dire che il tempo quadro è quello che permette al nostro osservatore di poter accelerare in modo costante. Per avere un’accelerazione che possa esser variabile con il tempo, serve un tempo 3D. Per capire quest’affermazione, pensiamo alla legge di gravitazione universale. Tale legge dice che due corpi di massa M1 ed M2, posti a distanza r, si attraggono con una forza pari a:
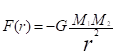
dove G è la costante di gravitazione universale di Newton.
Tale legge, come si può vedere, è espressa in funzione della distanza r. Si vede subito che in tale formula, non compare il tempo. Questa formula ci dice cosa succede fra due corpi di massa M1 ed M2 posta ad una distanza fissa r. Ciò vuol dire che la suddetta relazione si riferisce al caso in cui i due corpi sono vincolati, ovvero c’è qualcosa che li blocca entrambi, impedendo loro di muoversi liberamente. Se invece volessimo il caso più complesso di due corpi non vincolati, dovremmo prendere in considerazione anche il tempo. Infatti, con il passare del tempo, e mano a mano che i due corpi si avvicinano l’un l’altro, la distanza tende a diminuire e la forza tende ad aumentare. Quindi potremmo dire che in quel caso l’accelerazione di gravità non sarebbe costante nel tempo, ma aumenterebbe con il tempo. Avremmo quindi la variazione di accelerazione al variare del tempo. Se l’accelerazione è il rapporto fra uno spazio e il quadrato del tempo, la variazione di accelerazione è il rapporto fra uno spazio è il tempo al cubo. Ecco che la suddetta legge, per avere una valenza dinamica in assenza di vincoli, deve richiedere un tempo 3D. Qualcuno potrebbe pensare che sono solo artifici matematici e ciò non implica necessariamente l’esistenza di un tempo 3D. Il fatto di dividere uno spazio per un tempo 3D ed ottenere un risultato diverso da zero, non vuol dire per forza che il tempo abbia la tridimensionalità come lo spazio. E’ indubbio però che ogni volta che operiamo una scelta, ci indirizziamo verso un determinato tipo di futuro. Ad ogni istante della nostra vita sappiamo che dinnanzi a noi ci si pone la libertà di scelta per qualunque cosa. Una volta che la scelta è stata fatta abbiamo indirizzato noi stessi e tutto ciò che avrà a che fare con noi in una determinata direzione. Gli altri possibili futuri che abbiamo scartato, che fine hanno fatto? Esistevano davvero nel momento in cui dovevamo scegliere, oppure era solo pura illusione? I cosiddetti “universi alternativi” non potrebbero essere una conseguenza di un tempo 3D? Se le cose stessero in questo modo, per il teorema della vista, un osservatore che appartenesse ad una dimensione ancora superiore non solo vedrebbe il futuro realmente intrapreso da ciascuno di noi, ma anche tutti i possibili futuri che avevamo a disposizione e che non abbiamo scelto. Potrebbe conoscere le conseguenze di ciascuno di quegli universi alternativi e quindi saprebbe sempre qual è il percorso migliore per ogni osservatore.
Ma cosa più importante, vista l’equivalenza accelerazione-gravità, e visto inoltre che la gravità è in grado di deformare lo spaziotempo stesso, ne consegue che l’introduzione di una sesta dimensione permette la distorsione dello spaziotempo e quindi di generare la massa. Quindi mentre una sola dimensione del tempo consente di distorcere le tre dimensioni dello spazio permettendo così il movimento dell’osservatore nello spazio stesso, analogamente una quinta dimensione permette l’accelerazione dei corpi e la sesta consente l’esistenza della gravitazione universale. Questa particolarità “attiva” al nostro osservatore la possibilità di avere le forze. Però queste sei dimensioni da sole non bastano per avere le forze; potremmo dire che le sei dimensioni sono una condizione necessaria ma non sufficiente per avere la materia. Occorre qualcos’altro affinché queste forze si manifestino, ovvero servono altre dimensioni che possano manipolare le precedenti 6 dimensioni.
Pertanto, sempre per analogia, se aggiungessimo la settima dimensione potremmo consentire al nostro osservatore di muoversi liberamente nel tempo 3D.
La Settima, l’ottava e la nona dimensione
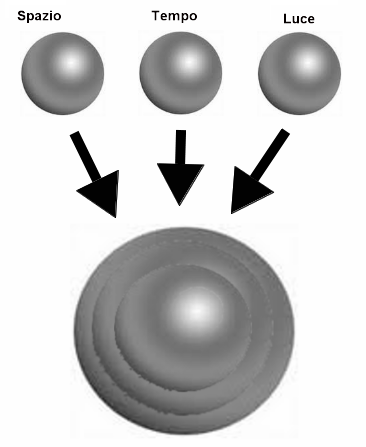
Per analogia alle 3 dimensioni dello spazio e alle 3 del tempo, abbiamo pensato che possa esistere un’ulteriore classe di dimensioni. Ancora una volta ci aspettavamo una terna tridimensionale. Ma cosa fosse questa terna ci è sembrato un mistero. Poi abbiamo pensato che non potendo percepire queste dimensioni in modo diretto, probabilmente ne avremmo percepito la presenza come un fenomeno fisico ordinario. Un fenomeno che probabilmente deve essere sempre uguale a se stesso indipendentemente da dove lo si osserva. Questo modo di ragionare ci ha portati automaticamente alle onde elettromagnetiche. Infatti la velocità della luce è costante ed è uguale in tutti i sistemi di riferimento. In questo caso chiameremo questa terna con il nome di “classe luce”. La cosa c’è sembrata a dir poco strana, ma poi abbiamo cercato di mettere da parte i pregiudizi ed abbiamo provato ad approfondire l’idea. In effetti, se ci si pensa bene, le onde elettromagnetiche hanno tre componenti fondamentali (elettricità, magnetismo e direzione di propagazione; si veda il capitolo “Luce e Materia”) e queste componenti potrebbero essere la traccia di una terna dimensionale o più. Ovviamente nel nostro spazio possono presentarsi solo come fenomeno fisico, come ci insegna il Teorema della Vista, ma la cosa potrebbe presentare degli aspetti interessanti. Anzi questa visione ci porta a pensare ad un mondo fatto da almeno 9 dimensioni, che per effetto di qualche vincolo strano ci permette di percepire tutte e 3 le dimensioni spaziali, ma d’altra parte ci limita a renderci conto della presenza delle 3 dimensioni del tempo facendole apparire come una sola. Per finire ci mostra la classe luce come un fenomeno fisico dello spaziotempo e non come una terna dimensionale. E’ anche possibile che la luce non sia una classe di sole 3 dimensioni spaziali. Questa ulteriore osservazione nasce dal fatto che la luce è un fenomeno dinamico e pertanto l’introduzione di sole tre dimensioni di tipo spazio non sia sufficiente a descriverla. Può darsi che in realtà sia costituita anch’essa da 3 dimensioni spaziali e 3 dimensioni temporali. In tal caso, poiché le dimensioni spazio e tempo sono già occupate, queste 6 dimensioni aggiuntive devono manifestarsi come una vibrazione di quelle già esistenti. In tal caso, sempre muovendoci sulla base di queste ipotesi, l’universo avrebbe 12 dimensioni e per il teorema della vista se ne potrebbero percepire soltanto n-1, cioè 11. Riprenderemo questo discorso in seguito quando parleremo della materia creata dai fotoni. Per ora vuol essere solo un’anticipazione per fare intravedere al lettore che questi discorsi non sono in disaccordo con le teorie che oggi vanno per la maggiore, come la teoria delle stringhe. Certo hanno punti di vista differenti, come ad esempio la compattazione delle dimensioni, ma vedrete in seguito come in realtà queste ipotesi aggiungono informazioni non banali.
Cosa interessante da osservare che in basa al Teorema della Vista, l’attivazione dei “gradi di libertà” su una nuova classe dimensionale abilitano il nostro osservatore a delle nuove capacità. Quindi, se i nostri ragionamenti fossero corretti, attivando i gradi di libertà nella classe di dimensione luce, l’osservatore avrebbe la possibilità di manipolare tutte le 6 dimensioni inferiori, creando materia e antimateria. Questa osservazione ci conforta perché la creazione di coppie materia-antimateria a partire dai fotoni ad alta energia, avviene proprio negli acceleratori di particelle.
Ovviamente, poiché ci stiamo muovendo su un terreno totalmente ignoto, ci teniamo a precisare che tutte queste cose vanno prese come ipotesi e non come una teoria scientifica dimostrata sperimentalmente. Si tratta di spunti di riflessione, anche se a rivederli più volte sembrano qualcosa di più che semplici osservazioni. Dopo la nona (o dodicesima) dimensione ci saranno altre classi e altre dimensioni in base al teorema della vista, ma la nostra “lungimiranza” per adesso finisce qui.
[1] http://it.wikipedia.org/wiki/Teoria_della_relatività
[2] Paradosso di Einstein-Podolsky-Rosen – http://it.wikipedia.org/wiki/Paradosso_EPR
[3] https://arxiv.org/abs/quant-ph/0510010
[4] http://it.wikipedia.org/wiki/D%C3%A9j%C3%A0_vu