L’argomento che sarà trattato nel prossimo capitolo, potrà sembrare ad alcuni lettori una rivisitazione delle idee di Edwin Abbott [1]Abbott, che nel lontano 1884 scrisse un racconto fantastico intitolato Flatilandia. In realtà, questa sensazione è solo apparente, perché come vedrete più avanti, il nostro interesse è legato ad un aspetto scientifico; quello di Abbott è più un interesse narrativo. Di fatto, Flatilandia, è un libro di satira politica in cui l’autore beffeggia la gretta società inglese dell’800. I personaggi principali, sono delle figure geometriche piane, come triangoli, quadrati, pentagoni, esagoni, ecc. e circonferenze. Nel mondo di Flatilandia, vige la legge che le caste superiori sono formate da poligoni regolari, cioè figure geometriche che hanno tutti i lati uguali, mentre il rango sociale è legato al numero di lati che esso possiede; tanto maggiore è il numero dei lati, tanto più è elevato il rango. Si passa così da quello più basso (i triangoli, con solo tre lati) a quello più alto (la circonferenza, che possiede un’infinità di lati); le donne di Flatilandia sono dei segmenti, cioè inferiori a tutti gli esseri di quest’insolito mondo. E’ questa la ragione che permette di collocare in modo univoco il racconto di Abbott, fra la satira politica. Il racconto, poi, prosegue con la storia di un quadrato, che un giorno finisce per incontrare la sfera. Questa, gli dimostra che essa può entrare ed uscire da una stanza, attraverso quella dimensione che il quadrato non riesce a vedere. Egli nonostante la dimostrazione, non crede alla sfera. Un giorno s’imbatte nel fantastico mondo di Linelandia, dove tutti gli abitanti sono dei segmenti. A questo punto, scartata l’ipotesi di aver incontrato una fila di donne del mondo Flatilandia, si rende conto che ciò che gli aveva detto la sfera era esatto; potevano esistere dimensioni che non potevano essere percepite. Il quadrato inizia a fantasticare sulle dimensioni superiori e immagina mondi a quattro o a cinque dimensioni. Il resto del libro è soltanto un approfondimento dei problemi del quadrato, che viene messo in prigione per le sue affermazioni e rischia di essere ucciso.
Altri lettori, si renderanno conto che lavori più o meno simili erano già stati condotti da Platone[2] in epoca più remota. Egli, infatti, cercava di immaginare come si poteva far credere a delle persone normali, di essere bidimensionali. Immaginò che degli uomini fossero incatenati fin dalla nascita all’interno di una caverna e che a causa delle catene, non potevano muovere nemmeno la testa. Inoltre, suppose che dietro a loro ci fosse un fuoco che proiettasse la loro ombra sulla parete di fronte a loro. Alla fine, non potendo vedere altro che ombre, si sarebbero identificati con le ombre stesse, credendo che il mondo fosse in realtà a due dimensioni.
Altri autori più recenti hanno poi affrontato l’argomento. Tra questi ci sono il Prof. Rudy Rucker[3] della San José University e il Prof. Thomas Banchoff[4] della Brown University; entrambe insegnano matematica nelle rispettive università. Il loro approccio con quest’argomento è senza dubbio affascinante. Per questi autori, esistono delle dimensioni superiori, ma secondo loro si misurano in metri. Sì, è possibile pensare ad una quarta dimensione geometrica che si misura ancora una volta in metri, come le tre precedenti, ma allora il tempo cos’è? E’ o non è una dimensione? Se è una dimensione, allora non può che essere la quarta; se non è una dimensione, viene meno tutto il discorso fatto da Einstein[5] sul continum spazio-tempo, nonché tutta la geometria di Minkowski[6] che è legata a questo discorso.
Un altro autore importante che si è occupato sulle dimensioni, è Stephen Hawking[7]. Nel suo Best-Seller “Dal Big Bang ai buchi neri”, ad un certo punto introduce la “Teoria delle Supercorde”. Nata da un’idea del fisico italiano Gabriele Veneziano[8], con il nome di “Teoria delle Corde”, si è poi sviluppata nell’ultimo decennio grazie ai contributi dei fisici Micheal Green[9] e John Schwarz[10]. Questa teoria riesce a dimostrare una notevole quantità di fenomeni fisici, soltanto se si suppone che l’universo abbia 20 o 30 dimensioni. Ma dove sono tutte le altre dimensioni che non vediamo? Secondo il resoconto di Hawking, (che ci espone la teoria Kaluza-Klein sulla compattazione dimensionale ) sarebbero tutte arrotolate o incurvate su loro stesse in un mondo infinitamente microscopico. In un primo momento, questa ipotesi appare plausibile, ma se ci si ferma a riflettere ci si rende conto che c’è un enorme errore di fondo: questo modo di pensare è tipico di un essere che ragiona in tre dimensioni… più avanti chiariremo meglio questo punto. Pertanto, l’ipotesi Kaluza-Klein[11], lascia molta perplessità, anche perché viene spontaneo chiedersi: perché soltanto quattro dimensioni percettibili e tutte le altre arrotolate?… perché le dimensioni percettibili debbono essere spazio e tempo?…. Cosa sono le altre dimensioni? Queste ed altre domande pongono in seria discussione tale l’ipotesi. Secondo Hawking, sarebbe assurdo pensare ad organismi a due dimensioni, in quanto il loro apparato digerente li dividerebbe completamente a metà. In altre parole, egli si preoccupa di sapere come possano esistere degli organismi biologici in mondi a dimensioni inferiori o superiori. Ma a noi tutto questo non interessa.
A dire il vero, quando abbiamo sviluppato i concetti che seguivamo, ignoravamo totalmente l’esistenza di altri lavori su quest’argomento. L’idea di verificare che queste intuizioni fossero originali, è venuta soltanto dopo, per evitare di sviluppare ulteriormente un lavoro che qualcuno poteva aver già fatto.
E’ stata una sorpresa scoprire che Platone avesse utilizzato la similitudine tra le varie dimensioni, e ci siamo meravigliati di più quando Abbott ideò Flatilandia, ma gli sviluppi più recenti sugli spazi a più dimensioni ci hanno fatto capire che le mie idee erano davvero innovative.
Tra questi, c’è anche il Prof. Antonio Zichichi[12], che dichiarò in un’intervista di molti anni fa (“Speciale TG1”, di RAIUNO) che secondo lui il nostro universo era composto da 43 dimensioni (11+32). Il fatto che lui attribuisse questo risultato ad una ricerca teorica, o meglio a dei calcoli da lui eseguiti e che facesse un gran mistero sulle dimensioni superiori, ci ha fatto pensare che molto probabilmente il suo risultato era conseguenza di un perfezionamento della teoria delle “superstringhe”. Però, con questa supposizione, non si sa di che “natura” sono queste ipotetiche dimensioni, per cui abbiamo dedotto che lui e la sua équipe, non avessero la più pallida idea di cosa fossero queste dimensioni. Comunque sia, il Prof. Zichichi ha affermato che l’universo a 43 dimensioni sarà una realtà della scienza moderna soltanto quando sarà scoperta una “superparticella”. Auguriamo di tutto cuore al Prof. Zichichi di trovarla, ma noi preferiamo percorre tutt’altra strada.
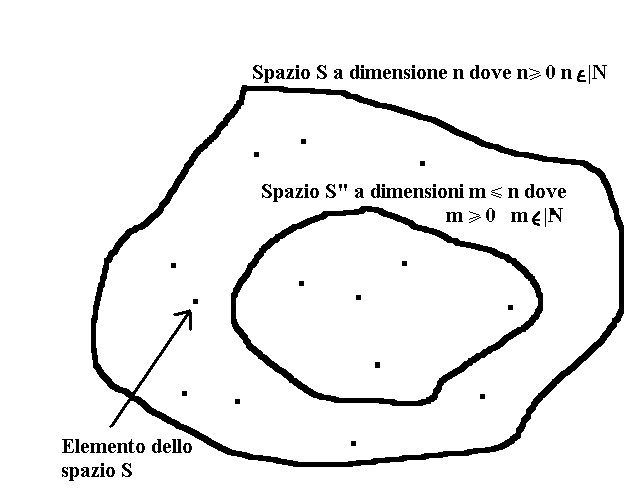
Prima di passare al primo capitolo, dobbiamo fare una piccola digressione, a favore di quei lettori che non hanno delle buone basi di matematica, gli altri, possono passare avanti. Invece, questi lettori, per capire alcuni concetti che saranno illustrati tra breve, devono aver ben chiaro il concetto di spazio e sottospazio. Quando si parla di “spazio S a n dimensioni”, s’intende dire che lo spazio (che non è solo quello che si misura in “metri”, ma possono essere anche “secondi” o quant’altro possa passare per la testa) ha un certo numero di dimensioni, che noi non conosciamo e che per comodità indichiamo con la lettera n. Questo numero è intero, e può essere compreso tra zero ed un numero infinitamente grande; però il fatto è che non c’interessa per ora sapere il suo valore, ma soltanto che esiste. Inoltre, tutti gli elementi dello spazio S, devono soddisfare certe proprietà, affinché S possa essere considerato uno “spazio”. Questo concetto può sembrare un po’ ostico ed astratto, ma se il lettore si fermerà un attimo a pensare, lo vedrà con più naturalezza. Invece, il concetto di sottospazio è molto più semplice e più facile da capire. Si può dire che alcuni elementi di S, formano un sottospazio, quando soddisfano quelle proprietà che permettono di considerare quegli stessi elementi come uno spazio a sé. E’ ovvio che il sottospazio di “S” è contenuto nello spazio S, ed ha una dimensione m, che è senz’altro minore o uguale a n.
I ragionamenti che faremo nel primo capitolo, possono essere fatti in virtù del fatto che uno spazio di dimensione m, può essere in ogni caso considerato come sottospazio di uno spazio n, con nmaggiore dim. In particolare considereremo degli spazi a dimensione uno, due e tre, che sono dei sottospazi di uno spazio a quattro dimensioni, cioè contenuti all’interno del nostro spazio quadrimensionale.
[1] http://it.wikipedia.org/wiki/Edwin_Abbott_Abbott
[2] http://it.wikipedia.org/wiki/Platone
[3] http://it.wikipedia.org/wiki/Rudy_Rucker
[4] http://en.wikipedia.org/wiki/Thomas_Banchoff
[5] http://en.wikipedia.org/wiki/Einstein
[6] http://en.wikipedia.org/wiki/Hermann_Minkowski
[7] http://en.wikipedia.org/wiki/Stephen_Hawking
[8] http://en.wikipedia.org/wiki/Gabriele_Veneziano
[9] http://en.wikipedia.org/wiki/Michael_Green_%28physicist%29
[10] http://en.wikipedia.org/wiki/John_Henry_Schwarz
[11] http://en.wikipedia.org/wiki/Kaluza-Klein
[12] http://it.wikipedia.org/wiki/Antonino_Zichichi